A helicopter flying along the path y=7+x32, A soldier standint at point (12,7) wants to hit the helicopter when it is closest from him, then minimum distance is equal to
a. 12
b. 13√73
c. 16√73
d. √56
The correct Answer is:C
To solve the problem, we need to find the minimum distance between the soldier standing at point (12,7) and the helicopter flying along the path given by the equation y=7+x32.
Step 1: Define the coordinates of the helicopter
Let the coordinates of the helicopter be P(α,7+α32), where α is the x-coordinate of the helicopter's position.
Step 2: Write the distance formula
The distance D between the soldier at point A(12,7) and the helicopter at point P(α,7+α32) can be expressed using the distance formula:
D=√(α−12)2+(7+α32−7)2
This simplifies to:
D=√(α−12)2+(α32)2
D=√(α−12)2+α3
Step 3: Minimize the distance
To minimize D, we can minimize D2 (since the square root function is monotonically increasing):
D2=(α−12)2+α3
Step 4: Differentiate D2
Now, we differentiate D2 with respect to α:
d(D2)dα=2(α−12)+3α2
Step 5: Set the derivative to zero
Setting the derivative equal to zero to find critical points:
2(α−12)+3α2=0
3α2+2α−1=0
Step 6: Solve the quadratic equation
Using the quadratic formula α=−b±√b2−4ac2a:
Here, a=3, b=2, and c=−1:
α=−2±√22−4⋅3⋅(−1)2⋅3
=−2±√4+126
=−2±√166
=−2±46
This gives us two possible values for α:
α1=26=13,α2=−66=−1(not valid since α≥0)
Step 7: Find the coordinates of point P
Using α=13:
y=7+(13)32=7+1√27=7+13√3
So, the coordinates of point P are (13,7+13√3).
Step 8: Calculate the minimum distance
Now, we can calculate the minimum distance D using the distance formula:
D=
⎷(13−12)2+(7+13√3−7)2
=
⎷(−16)2+(13√3)2
=√136+127
Finding a common denominator (which is 108):
=√3108+4108=√7108=√76√3=√2118
Thus, the minimum distance is √2118.
Let the coordinates of the helicopter be P(α,7+α32), where α is the x-coordinate of the helicopter's position.
The distance D between the soldier at point A(12,7) and the helicopter at point P(α,7+α32) can be expressed using the distance formula:
D=√(α−12)2+(7+α32−7)2
This simplifies to:
D=√(α−12)2+(α32)2
D=√(α−12)2+α3
To minimize D, we can minimize D2 (since the square root function is monotonically increasing):
D2=(α−12)2+α3
Now, we differentiate D2 with respect to α:
d(D2)dα=2(α−12)+3α2
Setting the derivative equal to zero to find critical points:
2(α−12)+3α2=0
3α2+2α−1=0
Using the quadratic formula α=−b±√b2−4ac2a:
Here, a=3, b=2, and c=−1:
α=−2±√22−4⋅3⋅(−1)2⋅3
=−2±√4+126
=−2±√166
=−2±46
This gives us two possible values for α:
α1=26=13,α2=−66=−1(not valid since α≥0)
Using α=13:
y=7+(13)32=7+1√27=7+13√3
So, the coordinates of point P are (13,7+13√3).
Now, we can calculate the minimum distance D using the distance formula:
D=
⎷(13−12)2+(7+13√3−7)2
=
⎷(−16)2+(13√3)2
=√136+127
Finding a common denominator (which is 108):
=√3108+4108=√7108=√76√3=√2118
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 6
6 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 7
8 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 4
6 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)
2 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
An Apache helicopter of enemy is flying along the curve given by y=x2+7. A soldier, placed at (3, 7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
View SolutionFind the point on the curve y2=2x which is at a minimum distance from the point (1, 4) .
View SolutionThe distance between points (2,−7,3) and (−2,7,3) is:
View SolutionQ is the image of point P(1, -2, 3) with respect to the plane x−y+z=7. The distance of Q from the origin is.
View SolutionA helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
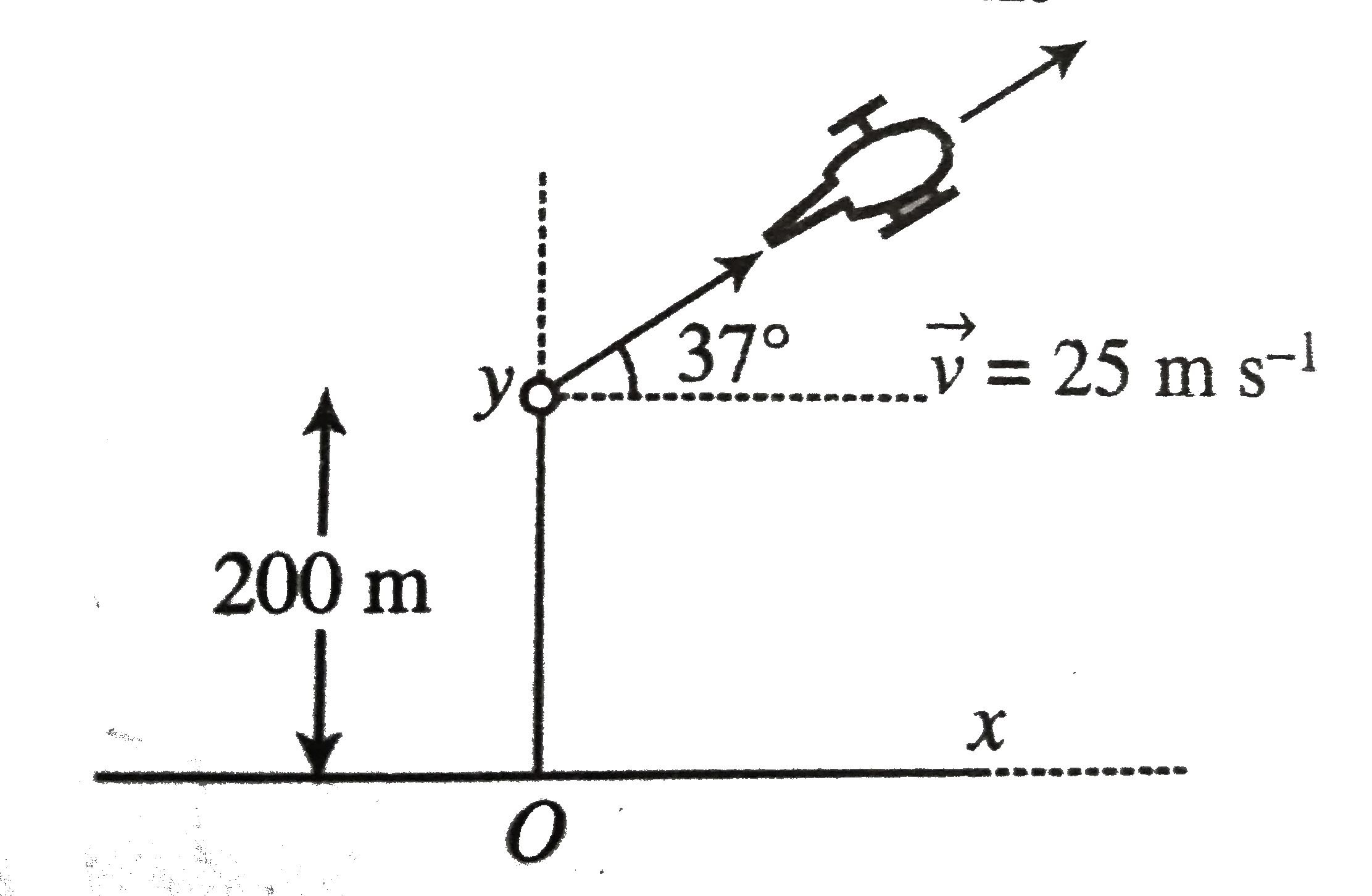
If the helicopter flies at constant velocity, find the x and y coordinates of the location of the helicopter when the package lands.
View SolutionA helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
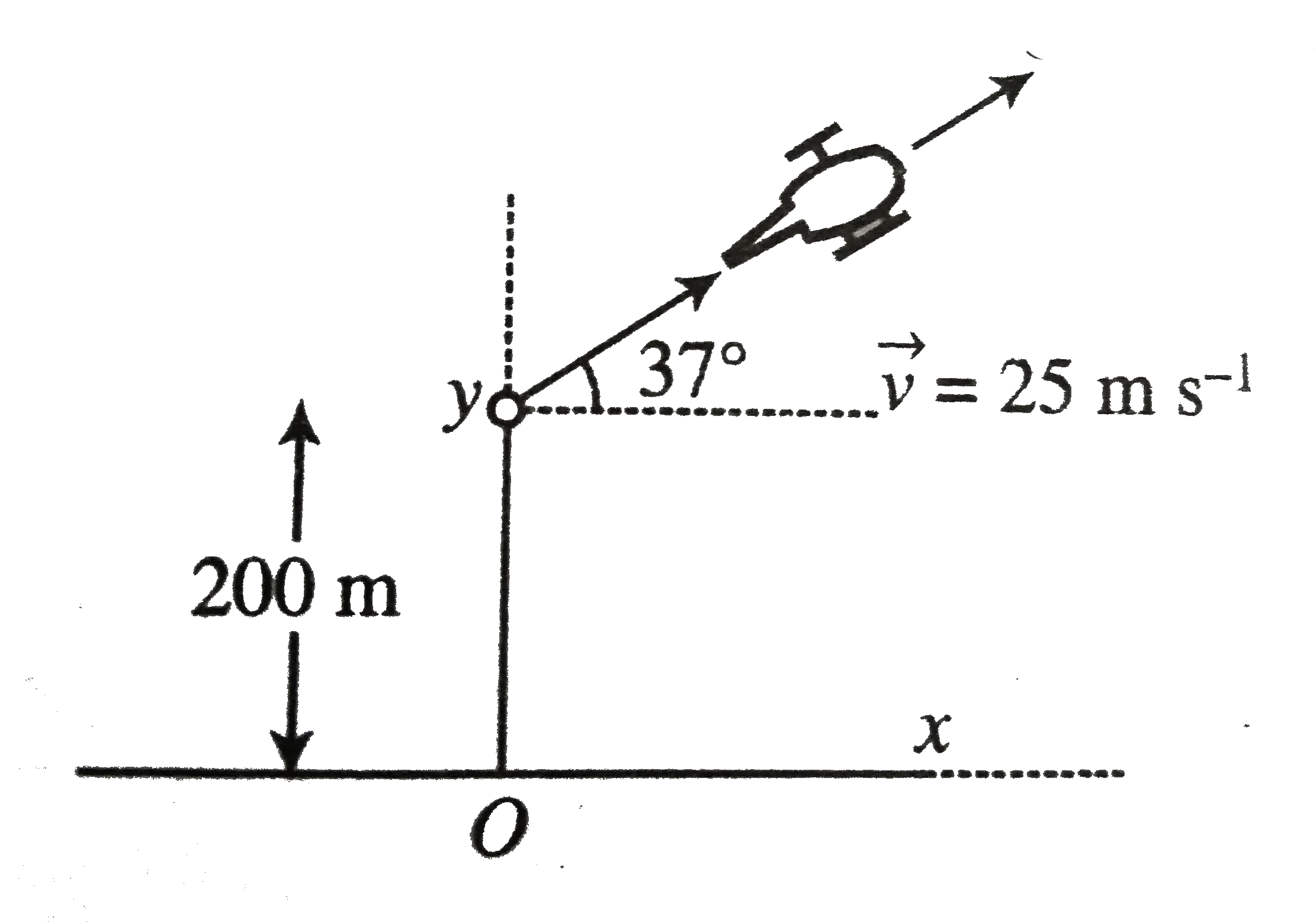
The distance of the point O where the package lands is
View SolutionA plane 2x+3y+5z=1 has a point P which is at minimum distance from line joining A(1,0,−3),B(1,−5,7), then distance AP is equal to
View SolutionA helicopter is moving verticallly upwards with a velocity 5ms−1. When the helicopter is at a height 10m from ground, a stone is thrown with a velocity (3ˆi+4ˆj)ms−1 from the helicopter w.r.t. the man in it. Considering the point on ground vertically below the helicopter as the origin of coordinates, and the ground below as xy plane, find the coordinates of the point where the stone will fall, its distance from origin at the instant the stone strikes the ground, assuming helicopter moves upwards with constant velocity.
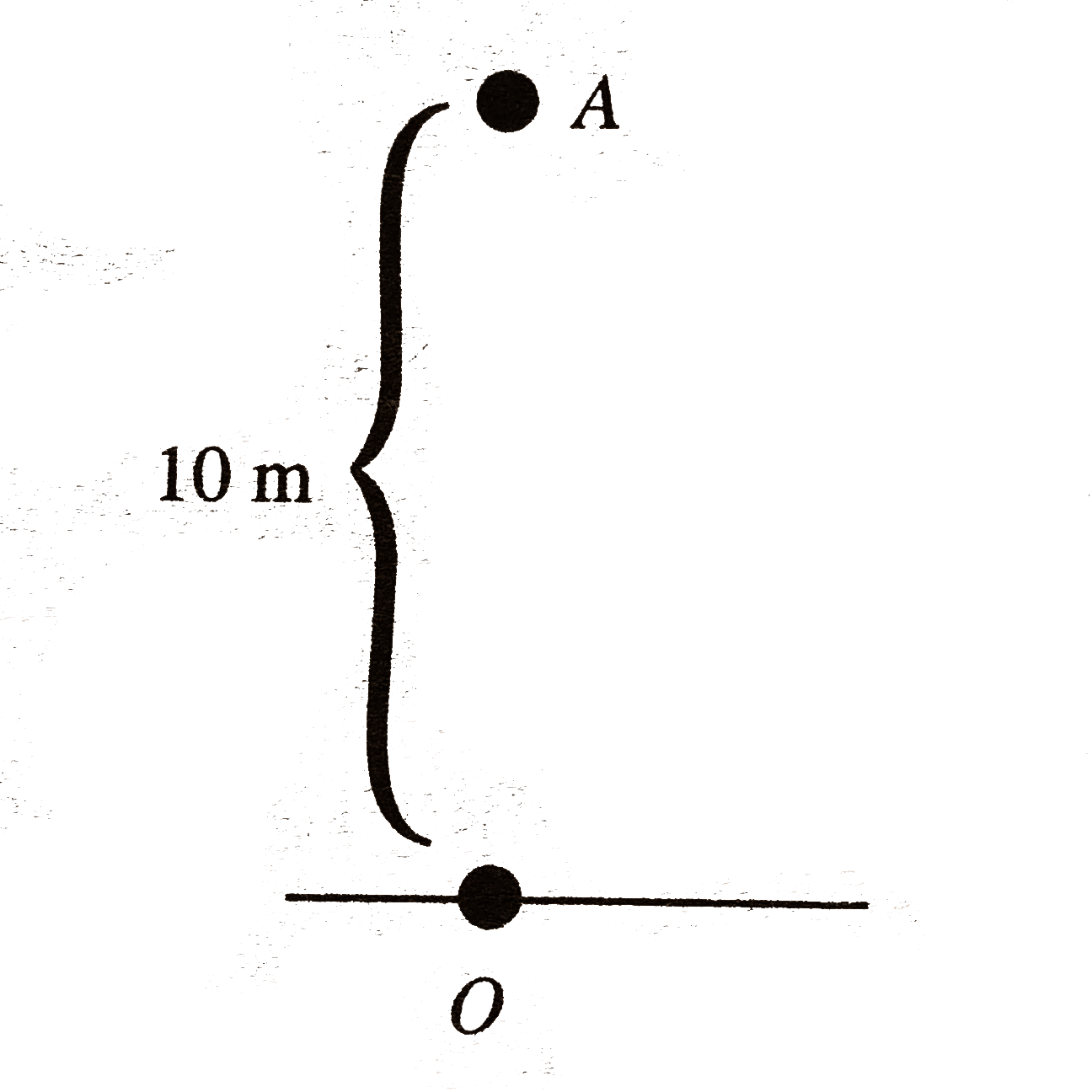 .
.
View SolutionThe distance between the points (1,3) and (x,7) is 5, find x.
View SolutionA jet of enemy is along the curve y=x2+2 and a soldier is placed at (3,2).Find the minimum distance between the jet and soldier.
View Solution
