The locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse x2a2+y2b2=1 forms a triangle of constant area with the coordinate axes is (a) straight line (b) a hyperbola (c) an ellipse (d) a circle
a straight line
a hyperbola
an ellipse
a circle
The correct Answer is:B
To solve the problem, we need to find the locus of a point from which the chord of contact of tangents drawn to the ellipse x2a2+y2b2=1 forms a triangle of constant area with the coordinate axes.
1. Equation of the Chord of Contact:
The equation of the chord of contact of tangents drawn from a point (h,k) to the ellipse is given by:
xx1a2+yy1b2=1
Substituting x1=h and y1=k, we have:
xha2+ykb2=1
2. Finding Intercepts:
To find the intercepts on the x-axis and y-axis:
- For the x-intercept (where y=0):
xha2=1⟹x=a2h
- For the y-intercept (where x=0):
ykb2=1⟹y=b2k
3. Coordinates of the Intercepts:
The intercepts on the axes are:
- A(a2h,0) on the x-axis
- B(0,b2k) on the y-axis
4. Area of the Triangle Formed:
The area A of the triangle formed by these intercepts and the origin (0,0) is given by:
Area=12×base×height=12×a2h×b2k
Therefore,
A=a2b22hk
5. Constant Area Condition:
Since the area is constant, we can set:
\frac{a^2 b^2}{2hk} = C \quad \text{(where C is a constant)}
Rearranging gives:
hk=a2b22C
Let k=a2b22Ch.
6. Identifying the Locus:
The equation hk=k0 (where k0=a2b22C) represents a rectangular hyperbola. Thus, the locus of the point (h,k) is a hyperbola.
Conclusion:
The locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse forms a triangle of constant area with the coordinate axes is a hyperbola.
The equation of the chord of contact of tangents drawn from a point (h,k) to the ellipse is given by:
xx1a2+yy1b2=1
Substituting x1=h and y1=k, we have:
xha2+ykb2=1
To find the intercepts on the x-axis and y-axis:
- For the x-intercept (where y=0):
xha2=1⟹x=a2h
- For the y-intercept (where x=0):
ykb2=1⟹y=b2k
The intercepts on the axes are:
- A(a2h,0) on the x-axis
- B(0,b2k) on the y-axis
The area A of the triangle formed by these intercepts and the origin (0,0) is given by:
Area=12×base×height=12×a2h×b2k
Therefore,
A=a2b22hk
Since the area is constant, we can set:
\frac{a^2 b^2}{2hk} = C \quad \text{(where C is a constant)}
Rearranging gives:
hk=a2b22C
Let k=a2b22Ch.
The equation hk=k0 (where k0=a2b22C) represents a rectangular hyperbola. Thus, the locus of the point (h,k) is a hyperbola.
The locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse forms a triangle of constant area with the coordinate axes is a hyperbola.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - MULTIPLE CORRECT ANSWERS TYPE18videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMOREHENSION TYPE21videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - CONCEPT APPLICATION EXERCISE 7.64videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type2videos
INDEFINITE INTEGRATION
Similar Questions
Find the locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse x2a2+y2b2=1 form a triangle of constant area with the coordinate axes.
View SolutionThe locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse x2a2+y2b2=1 forms a triangle of constant area with the coordinate axes is a straight line (b) a hyperbola an ellipse (d) a circle
View SolutionThe locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse x2a2+y2b2=1 forms a triangle of constant area with the coordinate axes is a straight line (b) a hyperbola an ellipse (d) a circle
View SolutionFind the locus of the point which is such that the chord of contact of tangents drawn from it to the ellipse x2a2+y2b2=1 form a triangle of constant area with the coordinate axes.
View SolutionLet the midpoint of the chord of contact of tangents drawn from A to the circle x2+y2=4 be M(1,−1) and the points of contact be B and C
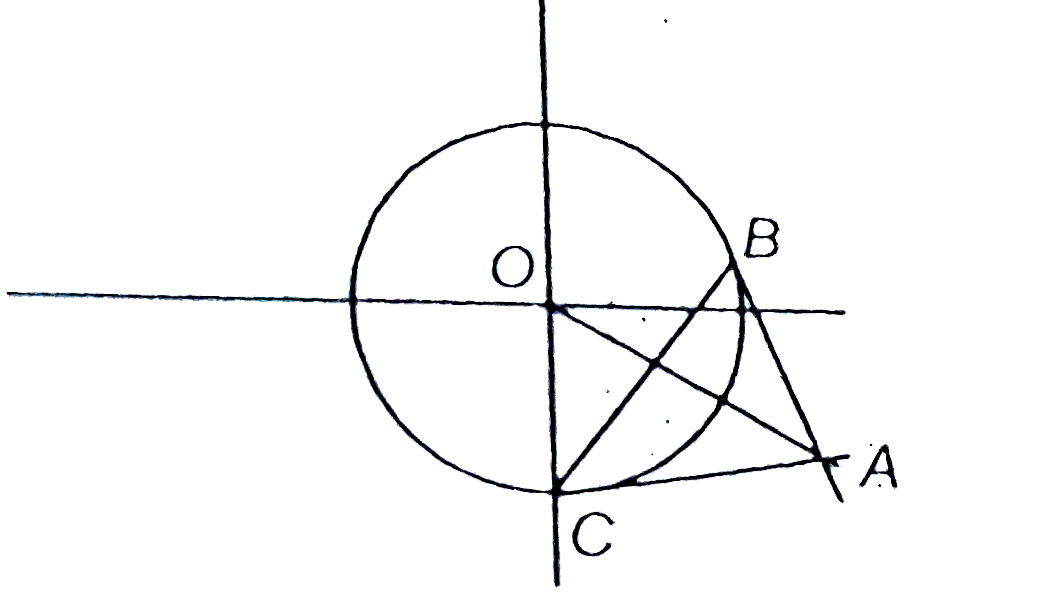 View Solution
View SolutionThe locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 which meet at right , is
View SolutionFind the locus of the foot of the perpendicular drawn from the center upon any tangent to the ellipse x2a2+y2b2=1.
View SolutionProve that the chords of contact of pairs of perpendicular tangents to the ellipse x2a2+y2b2=1 touch another fixed ellipse.
View SolutionProve that the chords of contact of pairs of perpendicular tangents to the ellipse x2a2+y2b2=1 touch another fixed ellipse.
View SolutionThe locus of mid-points of a focal chord of the ellipse x2a2+y2b2=1
View Solution

