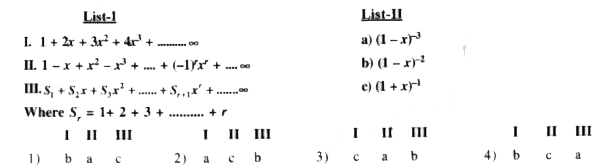Consider set $A = {T (r + 1) = .^{n} C_{r} {(3)}^{n - r} {(5 x)}^{r}, r = 0, 1, 23, \dots.., n}$ . Match the following lists :
$Consider set A = {T(r+1)=.^(n)C(r)(3)^(n-r)(5x)^(r), r = 0,1,23,$

Text Solution

Verified by Experts

The correct Answer is:3

a. If $T_{r + 1}$ is greatest , then $\frac{n}{1 + ∣ ∣ \frac{a}{b x} ∣ ∣} \leq r \leq \frac{n + 1}{1 + ∣ ∣ \frac{a}{b x} ∣ ∣}$
For $x = 1$ and $r = 11, \frac{n}{1 + \frac{3}{5}} \leq 11 \leq \frac{n + 1}{1 + \frac{3}{5}}$
$\Rightarrow 5 n \leq 88 \leq 5 (n + 1)$
$\Rightarrow n = 17$
(b) if $T (r + 1)$ is greatest ,then $(\frac{r}{n - r + 1}) \frac{a}{b} \leq x \leq (\frac{r + 1}{n - r}) \frac{a}{b}$
For $n = 25$ and $r = 20, 2 < x < \frac{63}{25}$
c. We have $\frac{T_{r + 1}}{T_{r}} = \frac{n - r + 1}{r} . \frac{b x}{a}$ for ${(a + b x)}^{n}$
For $n = 20$ and $r = 10, \frac{11}{10} . \frac{5 x}{3} = 1$ or $x = 6 / 11$
d. we have
$\frac{n}{1 + ∣ ∣ \frac{a}{b x} ∣ ∣} \leq r \leq \frac{n + 1}{1 + ∣ ∣ \frac{a}{b x} ∣ ∣}$ for ${(a + b x)}^{n}$ .
For $x = 2$ and $r = 8$ (as $T (9)$ will be largest).
$\frac{n}{1 + ∣ ∣ \frac{a}{b x} ∣ ∣} \leq 8 \leq \frac{n + 1}{1 + \frac{3}{10}}$
$\Rightarrow 10 n \leq 104 \leq 10 (n + 1)$
$\Rightarrow n = 10$

|

Updated on:21/07/2023

Class 12 MATHS BINOMIAL THEOREM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The vaule of $n - 1 \sum r = 0 (\frac{_{r}^{C_{r}}}{^{n} C_{r} +^{n} C_{r + 1}}$ is equal to
A $\frac{n}{2}$
B $\frac{n + 1}{2}$
C $\frac{n (n - 1)}{2 (n + 1)}$
D $\frac{n (n + 1)}{2}$
Question 2 - Select One
If $n \sum r = 0 {\frac{^{n} C_{r - 1}}{'^{n} C_{r} +^{n} C_{r - 1}}}^{3} = \frac{25}{24}$ , then $n$ is equal to
A $3$
B $4$
C $5$
D $6$

CENGAGE ENGLISH-BINOMIAL THEOREM-Matrix

Home
Ask Doubt
Profile