In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
If a students selected at random is found to have passed the examination, then the probability that he was the only student who has passed the examination is
1/3025
1/605
1/275
1/121
The correct Answer is:A
To solve the problem, we need to find the probability that a student who has passed the examination is the only student who passed, given that the probability of exactly i students passing is proportional to i2.
1. Define the Probability Function:
Let P(Ei) be the probability of exactly i students passing the examination. According to the problem, this probability is directly proportional to i2. Therefore, we can express this as:
P(Ei)=k⋅i2
where k is a constant of proportionality.
2. Calculate Total Probability:
The total probability for all possible outcomes (from 0 to 10 students passing) must equal 1. Thus, we have:
P(E0)+P(E1)+P(E2)+…+P(E10)=1
Substituting the expression for P(Ei):
k⋅(02+12+22+…+102)=1
The sum of squares from 0 to 10 can be calculated as:
02+12+22+…+102=10(10+1)(2⋅10+1)6=10⋅11⋅216=385
Thus, we have:
k⋅385=1⟹k=1385
3. Find Individual Probabilities:
Now we can find the probabilities for each case:
P(E0)=k⋅02=0
P(E1)=k⋅12=1385
P(E2)=k⋅22=4385
P(E3)=k⋅32=9385
P(E4)=k⋅42=16385
P(E5)=k⋅52=25385
P(E6)=k⋅62=36385
P(E7)=k⋅72=49385
P(E8)=k⋅82=64385
P(E9)=k⋅92=81385
P(E10)=k⋅102=100385
4. Calculate P(A):
Let A be the event that a student passes the examination. The probability of event A is given by:
P(A)=P(E1)+P(E2)+P(E3)+…+P(E10)
P(A)=1385+4385+9385+16385+25385+36385+49385+64385+81385+100385
P(A)=1+4+9+16+25+36+49+64+81+100385=385385=1
5. Find P(E1|A):
We need to find the conditional probability P(E1|A):
P(E1|A)=P(E1)P(A)=13851=1385
Final Answer:
Thus, the probability that a student who has passed the examination is the only student who passed is:
1385
Let P(Ei) be the probability of exactly i students passing the examination. According to the problem, this probability is directly proportional to i2. Therefore, we can express this as:
P(Ei)=k⋅i2
where k is a constant of proportionality.
The total probability for all possible outcomes (from 0 to 10 students passing) must equal 1. Thus, we have:
P(E0)+P(E1)+P(E2)+…+P(E10)=1
Substituting the expression for P(Ei):
k⋅(02+12+22+…+102)=1
The sum of squares from 0 to 10 can be calculated as:
02+12+22+…+102=10(10+1)(2⋅10+1)6=10⋅11⋅216=385
Thus, we have:
k⋅385=1⟹k=1385
Now we can find the probabilities for each case:
P(E0)=k⋅02=0
P(E1)=k⋅12=1385
P(E2)=k⋅22=4385
P(E3)=k⋅32=9385
P(E4)=k⋅42=16385
P(E5)=k⋅52=25385
P(E6)=k⋅62=36385
P(E7)=k⋅72=49385
P(E8)=k⋅82=64385
P(E9)=k⋅92=81385
P(E10)=k⋅102=100385
Let A be the event that a student passes the examination. The probability of event A is given by:
P(A)=P(E1)+P(E2)+P(E3)+…+P(E10)
P(A)=1385+4385+9385+16385+25385+36385+49385+64385+81385+100385
P(A)=1+4+9+16+25+36+49+64+81+100385=385385=1
We need to find the conditional probability P(E1|A):
P(E1|A)=P(E1)P(A)=13851=1385
Thus, the probability that a student who has passed the examination is the only student who passed is:
1385
Topper's Solved these Questions
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MATRIX MATCH TYPE
10 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
24 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CHOICE ANSWER TYPE
17 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Video
Similar Questions
In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
The probability that exactly 5 students passing an examination is
View SolutionIn a class of 10 student, probability of exactly i students passing an examination is directly proportional to i2. If a student is selected at random, then the probability that he has passed the examination is
View Solution
Knowledge Check
A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?A155B14C13D1128
There are n students in a class. Ler P(Eλ) be the probability that exactly λ out of n pass the examination. If P(Eλ) is directly proportional to λ2(0≤λ≤n).
If a selected student has been found to pass the examination, then the probability that he is the only student to have passed the examination, is
View Solution100 students appeared for two examinations. 60 passed the first, 50 passed the second and 30 passed both. Find the probability that a student selected at random has passed at least one examination.
View Solution100 students appeared for two examinations .60 passed the first , 50 passed the second and 30 passed both . Find the probability that a student selected at random has failed in both examinations .
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
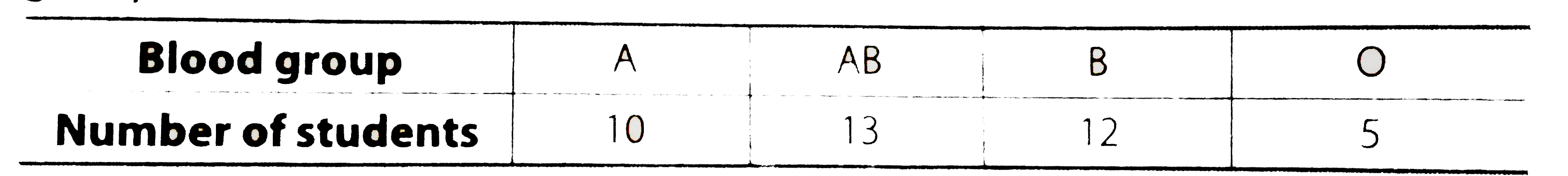
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionA class has 20 girls and 16 boys. One student is selected at random. Find the probability that the student is a girl.
View SolutionThere are 60 questions in a question paper. If no two students solve the same combination of questions but solve equal number of questions, then the maximum number of student who appeared in the examination, is
View SolutionA class consists of 50 students out of which there are 10 girls. In the class 2 girls and 5 boys are rank holders in an examination. If a student is selected at random from the class and is found to be a rank holder, what is the probability that the student selected is a girl?
View Solution