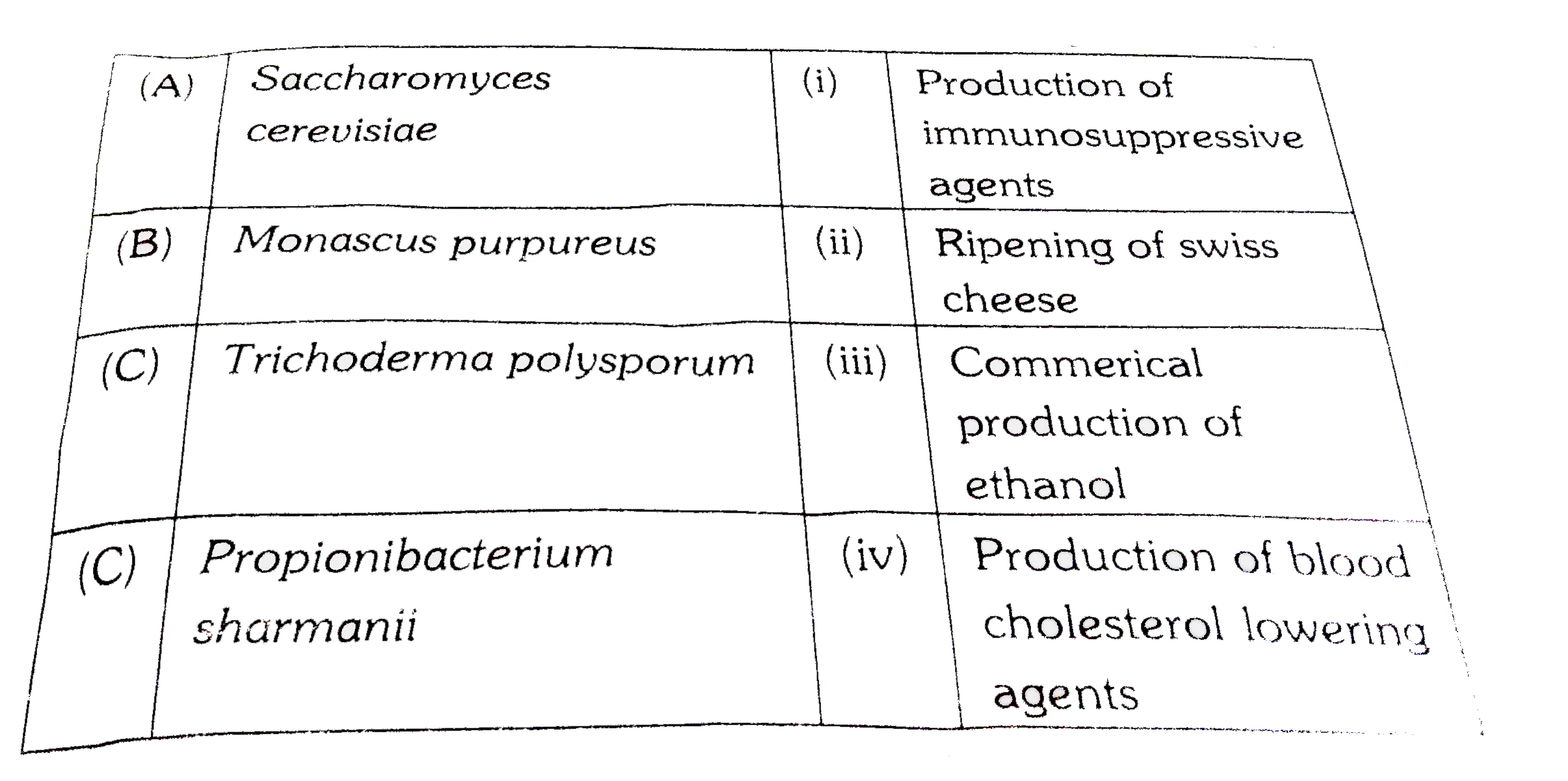Match the following lists:

a→p,b→q,r,c→s,r,d→q,r.
a. f(1−x)=f(1+x)
∴ −f'(1−x)=f'(1+x)
Hence, graph of f(x) is symmetrical about point (1, 0) [ as if f(x) = - f(-x), then f(x) is odd and its graphs is symmetrical about (0,0). Now shift the graph at (1,0)].
b. f(2−x)+f(x)=0
Replacexby1+x.Thenf(2−(1+x))+f(1+x)=0
or f(1−x)+f(1+x)=0
or −f'(1−x)+f'(1+x)=0
or f'(1−x)=f'(1+x) (1)
Therefore, graph of f'(x) is symmetrical about line x=1.
Alos, put x=2 in (1). Then f'(-1)=f'(3).
c. f(x+2)+f(x)=0 (1)
Replace xbyx+2.thenf(x+4)+g(c+2)=0 (2)
From (1) and (2), we have f(x) = f(x+4)
Hence, f(x) is periodic with period 4.
Also, f'(x)=f'(x+4).
Hence, f'(x) is periodic with period 4.
Put =−1∈f'(x)=f'(x+4).Thenf'(−1)=f'(3).
d. Putting x=0,y=0,we≥t2f(0)+{f(0)}2=1
or f(0)=√2−1 [∵f(0)>0]
Putting y=x,2f(x)+{f(x)}2=1
Differentiating w.r.t. x, we get
2f'(x)+2f⋅f'(x)=0
or f'(x){1+f(x)}=0
or f'(x)=0, because f(x)>0.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Numerical Value Type45videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Archives14videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Linked Comprehension Type24videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type5videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.Ai−(B),ii−(C),iii−(D),iv−(A)Bi−(B),ii−(D),iii−(C),iv−(A)Ci−(D),ii−(C),iii−(B),iv−(A)Di−(D),ii−(A),iii−(C),−iv−(B)
Match the following list of bacteria and their commercially important products
Choose the correct match
 View Solution
View SolutionMatch the following list of bioactive sub- stances and their roles
Choose the correct match
 View Solution
View SolutionMatch the following list of animals with their level of organisation.
Choose the correct match sryowing division of labour with animal example.
 View Solution
View SolutionMatch the following list of animals with their level of organisation :
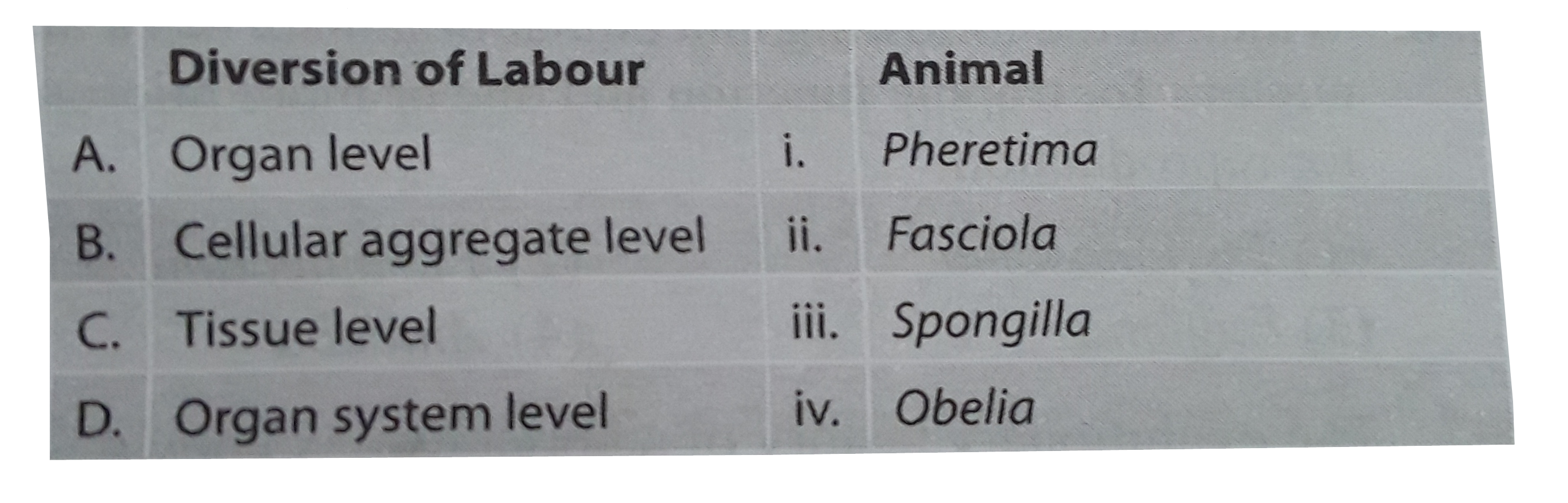
Choose the correct match showing division of labour with animals.View SolutionMatch the following list of bacteria and their commercially important products.
BacteriumProduct(i)Aspergillus niger(A)Lactic acid(ii)Acetobacter aceti(B)Butyric acid(iii)Clostridium butylicum(C)Acetic acid(iv)Lactobacillus(D)Citric acid
Choose the correct match.View SolutionMatch the following list of animals with their level of organisation.
Division of LabourAnimalA.Organ leveli.PheretimaB.Cellular aggregate levelii.FasciolaC.Tissue leveliii.SpongillaD.Organ system leveliv.Obelia
Choose the correct match showing division of labour with animal example.View SolutionMatch the following list of bioactive substances and their roles.
Bioactive substanceRole(i)Statin(A)Removal of oil stains(ii)CyclosporinA(B)Removal of clots from blood vessels(iii)Streptokinase(C)Lowering of blood cholesterol(iv)Lipase(D)Immuno-suppressive agent
Choose the correct match.View Solution