Two parabola have the same focus. If their directrices are the x-axis and the y-axis respectively, then the slope of their common chord is :
±1
4/3
3/4
none of these
The correct Answer is:A
To solve the problem, we need to find the slope of the common chord of two parabolas that have the same focus but different directrices. Let's break down the solution step by step.
Step 1: Define the Focus and Directrices
Let the focus of both parabolas be F(a,b). The directrix of the first parabola is the x-axis (which can be represented as y=0), and the directrix of the second parabola is the y-axis (which can be represented as x=0).
Step 2: Write the Equation of the First Parabola
Using the definition of a parabola, the distance from any point P(x,y) on the parabola to the focus F(a,b) is equal to the distance from P to the directrix.
For the first parabola (directrix is the x-axis):
PF=√(x−a)2+(y−b)2
The distance from point P to the x-axis (directrix) is simply y.
Setting these distances equal gives:
√(x−a)2+(y−b)2=y
Squaring both sides:
(x−a)2+(y−b)2=y2
Step 3: Simplify the Equation of the First Parabola
Expanding and simplifying:
(x−a)2+(y2−2by+b2)=y2
This simplifies to:
(x−a)2+b2−2by=0
Rearranging gives the equation of the first parabola:
(x−a)2+b2=2by
Step 4: Write the Equation of the Second Parabola
For the second parabola (directrix is the y-axis):
PF=√(x−a)2+(y−b)2
The distance from point P to the y-axis (directrix) is x.
Setting these distances equal gives:
√(x−a)2+(y−b)2=x
Squaring both sides:
(x−a)2+(y−b)2=x2
Step 5: Simplify the Equation of the Second Parabola
Expanding and simplifying:
(x−a)2+(y2−2by+b2)=x2
This simplifies to:
(x−a)2+b2−2by=x2
Rearranging gives the equation of the second parabola:
(x−a)2+b2=2bx
Step 6: Find the Common Chord
To find the common chord, we subtract the two equations derived from the parabolas:
((x−a)2+b2−2by)−((x−a)2+b2−2bx)=0
This simplifies to:
−2by+2bx=0
Factoring out 2:
2(bx−by)=0
Thus, we have:
bx=by
This implies:
y=x
and
y=−x
Step 7: Determine the Slope
The equations y=x and y=−x represent lines with slopes of 1 and −1, respectively. Therefore, the slopes of the common chord are:
slope=±1
Final Answer
The slope of their common chord is ±1.
---
Let the focus of both parabolas be F(a,b). The directrix of the first parabola is the x-axis (which can be represented as y=0), and the directrix of the second parabola is the y-axis (which can be represented as x=0).
Using the definition of a parabola, the distance from any point P(x,y) on the parabola to the focus F(a,b) is equal to the distance from P to the directrix.
PF=√(x−a)2+(y−b)2
The distance from point P to the x-axis (directrix) is simply y.
√(x−a)2+(y−b)2=y
Squaring both sides:
(x−a)2+(y−b)2=y2
Expanding and simplifying:
(x−a)2+(y2−2by+b2)=y2
This simplifies to:
(x−a)2+b2−2by=0
Rearranging gives the equation of the first parabola:
(x−a)2+b2=2by
For the second parabola (directrix is the y-axis):
PF=√(x−a)2+(y−b)2
The distance from point P to the y-axis (directrix) is x.
√(x−a)2+(y−b)2=x
Squaring both sides:
(x−a)2+(y−b)2=x2
Expanding and simplifying:
(x−a)2+(y2−2by+b2)=x2
This simplifies to:
(x−a)2+b2−2by=x2
Rearranging gives the equation of the second parabola:
(x−a)2+b2=2bx
To find the common chord, we subtract the two equations derived from the parabolas:
((x−a)2+b2−2by)−((x−a)2+b2−2bx)=0
This simplifies to:
−2by+2bx=0
Factoring out 2:
2(bx−by)=0
Thus, we have:
bx=by
This implies:
y=x
and
y=−x
The equations y=x and y=−x represent lines with slopes of 1 and −1, respectively. Therefore, the slopes of the common chord are:
slope=±1
The slope of their common chord is ±1.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWER TYPE )26videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - LINKED COMPREHENSION TYPE45videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.79videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension8videos
PERMUTATION AND COMBINATION
Similar Questions
The parabola having its focus at (3,2) and directrix along the Y-axis has its vertex at
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
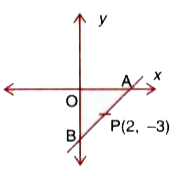
slope of line ABView SolutionTwo parabolas with a common vertex and with axes along x-axis and y-axis respectively, intersect each other in the first quadrant. If the length of the latus rectum of each parabola is 3, then the equation of the common tangent to the two parabolas is:
View SolutionLet there be two parabolas with the same axis, focus of each being exterior to the other and the latus rectam being 4a and 4b. The locus of the middle points of the intercepts between the parabolas made on the lines parallel to the common axis is a:
View SolutionP is parabola, whose vertex and focus are on the positive x axis at distances a and a' from the origin respectively, then (a'>a). Find the equation of parabola P.
View SolutionA circle of radius 4 drawn on a chord of the parabola y2=8x as diameter touches the axis of the parabola. Then the slope of the chord is
View SolutionA focal chord for parabola y2=8(x+2) is inclined at an angle of 60∘ with positive x-axis and intersects the parabola at P and Q. Let perpendicular bisector of the chord PQ intersects the x-axis at R, then the distance of R from focus is :
View SolutionA focal chord for parabola y2=8(x+2) is inclined at an angle of 60∘ with positive x-axis and intersects the parabola at P and Q. Let perpendicular bisector of the chord PQ intersects the x-axis at R, then the distance of R from focus is :
View SolutionLet A and B be two distinct points on the parabola y2=4x. If the axis of the parabola touches a circle of radius r having AB as its diameter, then find the slope of the line joining A and B .
View SolutionA movable parabola touches x-axis and y-axis at (0,1) and (1,0). Then the locus of the focus of the parabola is :
View Solution

