Match the following lists and then choose the correct code.

abcdprqq
abcdqprs
abcdspqr
abcdrsqp
The correct Answer is:B
2
a. We get common normal perpendicular to y=x.
So, slope =−1⇒x+y=3a
b. Tangent to the parabola y=mx+a/m passes through the point P(h,k).
⇒m2h−mk+a=0
If its roots are m1andm2, then m1m2−+1
Thus, locus is x=a.
c. The tangents are
y=m(x+a)+a/m (1)
andy=−1m(x+2a)−2am (2)
Subtracting (1) from (2), we get
x+3a=0
d. If chord joining t1andt1 subtends angle of 90∘ at vertex then t1t2=−4. Point of intersection of tangents is (−at1t1,−a(t1+t1)). So, the locus is x=4a.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - NUMERICAL VALUE TYPE32videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - ARCHIVES SINGLE CORRECT ANSWER TYPE8videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - LINKED COMPREHENSION TYPE45videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension8videos
PERMUTATION AND COMBINATION
Similar Questions
Match the following and choose the correct option
 View Solution
View SolutionMatch the following lists:
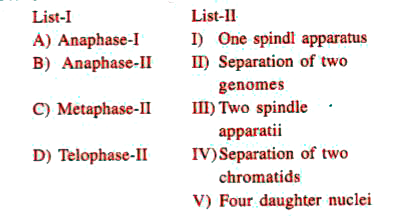
The correct match isView SolutionStudy the following list and find out the correct match
 View Solution
View SolutionStudy the following lists and find the correct match
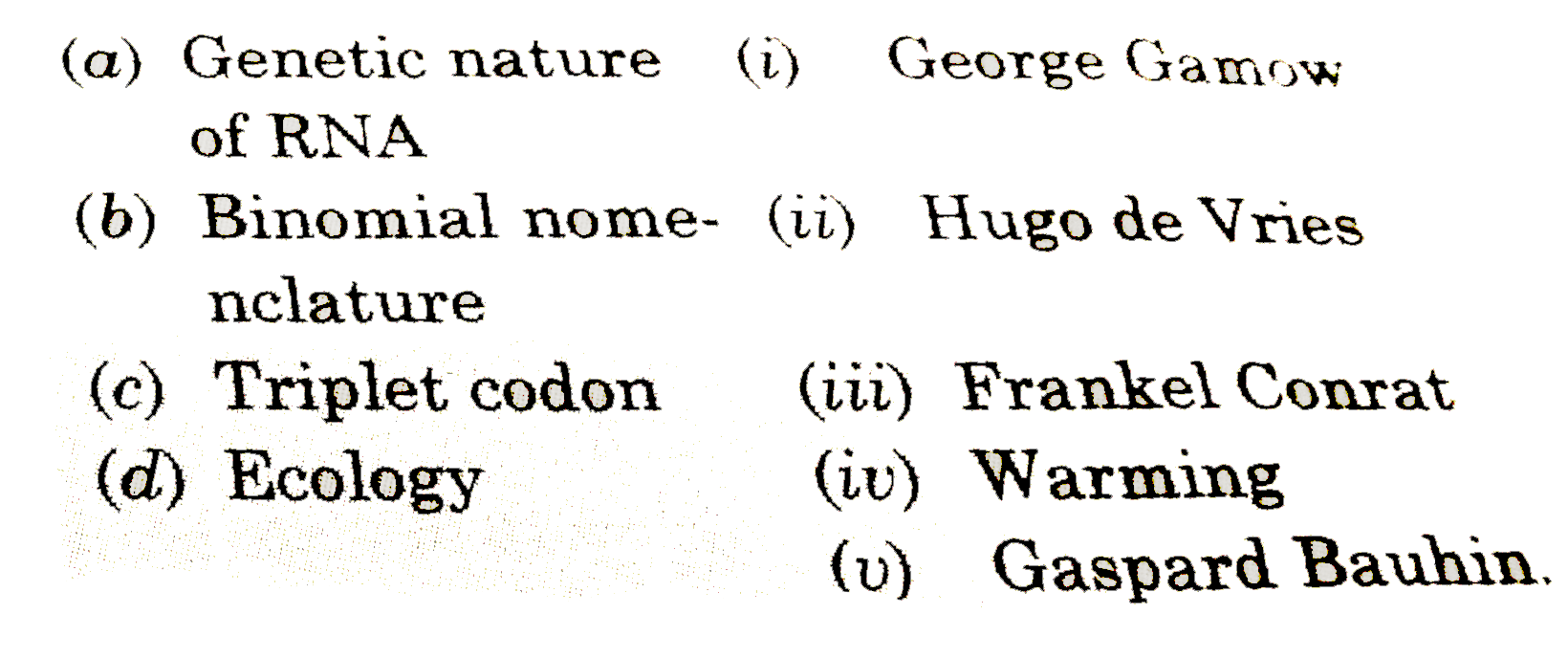 View Solution
View SolutionStudy the following lists and find the correct match
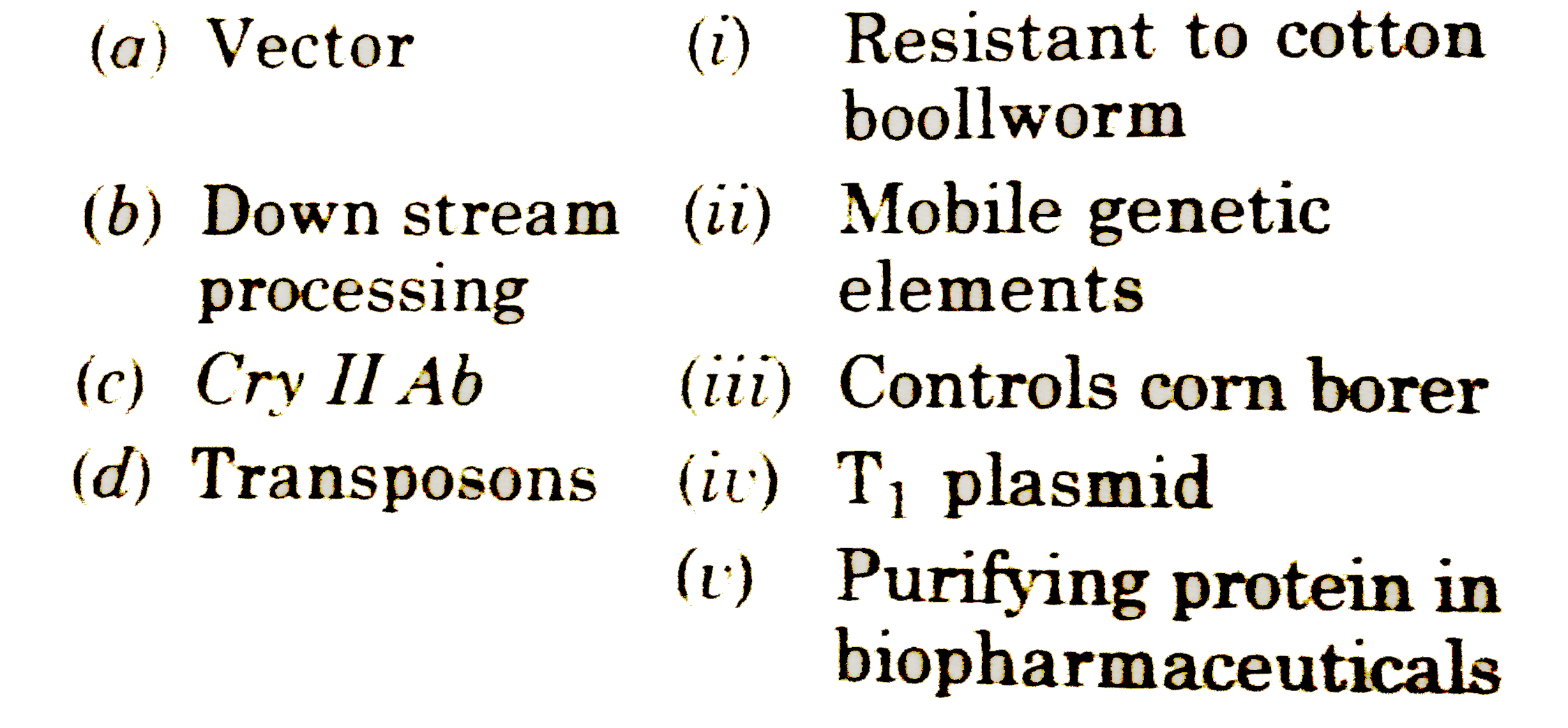 View Solution
View SolutionMatch correctly the following and choose the correct option.

The correct matches is:View SolutionMatch List I with List II and choose the correct answer
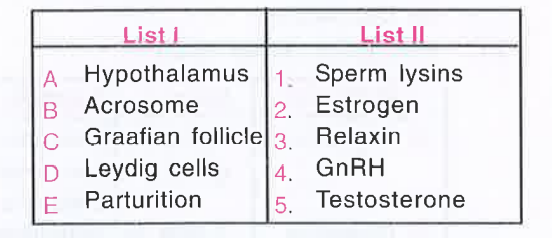 View Solution
View SolutionMatch the List with List II and choose the correct option from the codes given below:
 View Solution
View SolutionMatch list I with list II and choose the correct answer from the codes given below :
 View Solution
View SolutionMatch list I with list II and then select the correct answer from the codes given below
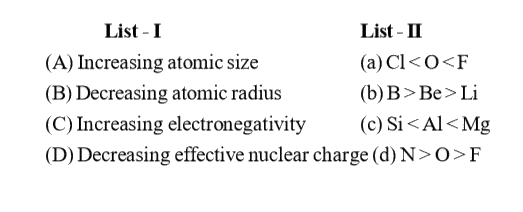
Codes :View Solution

