A particle acted on by constant forces 4→i+→j−3→kand3→i+→j−→k is displaced from the point →i+2→j+3→k to the point 5→i+4→j+→k. Find the total work done by the forces
To solve the problem step by step, we will follow these steps:
Step 1: Identify the Forces
We have two forces acting on the particle:
- →F1=4^i+^j−3^k
- →F2=3^i+^j−^k
Step 2: Calculate the Total Force
The total force →F acting on the particle is the sum of the two forces:
→F=→F1+→F2
Calculating this gives:
→F=(4^i+^j−3^k)+(3^i+^j−^k)=(4+3)^i+(1+1)^j+(−3−1)^k=7^i+2^j−4^k
Step 3: Identify the Displacement
The particle is displaced from point →d1=^i+2^j+3^k to point →d2=5^i+4^j+^k. The displacement →d is given by:
→d=→d2−→d1
Calculating this gives:
→d=(5^i+4^j+^k)−(^i+2^j+3^k)=(5−1)^i+(4−2)^j+(1−3)^k=4^i+2^j−2^k
Step 4: Calculate the Work Done
The work done W by the forces is given by the dot product of the total force →F and the displacement →d:
W=→F⋅→d
Calculating this gives:
W=(7^i+2^j−4^k)⋅(4^i+2^j−2^k)
Calculating the dot product:
W=(7×4)+(2×2)+(−4×−2)=28+4+8=40
Final Answer
The total work done by the forces is W=40 units.
---
We have two forces acting on the particle:
- →F1=4^i+^j−3^k
- →F2=3^i+^j−^k
The total force →F acting on the particle is the sum of the two forces:
→F=→F1+→F2
Calculating this gives:
→F=(4^i+^j−3^k)+(3^i+^j−^k)=(4+3)^i+(1+1)^j+(−3−1)^k=7^i+2^j−4^k
The particle is displaced from point →d1=^i+2^j+3^k to point →d2=5^i+4^j+^k. The displacement →d is given by:
→d=→d2−→d1
Calculating this gives:
→d=(5^i+4^j+^k)−(^i+2^j+3^k)=(5−1)^i+(4−2)^j+(1−3)^k=4^i+2^j−2^k
The work done W by the forces is given by the dot product of the total force →F and the displacement →d:
W=→F⋅→d
Calculating this gives:
W=(7^i+2^j−4^k)⋅(4^i+2^j−2^k)
Calculating the dot product:
W=(7×4)+(2×2)+(−4×−2)=28+4+8=40
The total work done by the forces is W=40 units.
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.1
18 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.2
15 Videos
- DETERMINANTSBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions
264 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type
5 Videos
Similar Questions
Knowledge Check
A particle acted upon by constant forces 4ˆi+ˆj−4ˆk and 3ˆi+ˆj−ˆk is displacment from the point ˆi+2ˆj+ˆk to point 5ˆi+4ˆj+ˆk.Total work done by the forces in SI unit is :
A20B40C50D30If →V=2→i+3→j and →Y=→i−5→j, the resultant vector of 2→U+3→V equals
A3→i−2→jB5→i+→jC7→i−9→jD8→i−→j
A paticle acted on by constant forces 4ˆi+ˆj−3ˆkand3ˆi+ˆj−ˆk is displaced from the point ˆi+2ˆj+3ˆk→5ˆi+4ˆj+ˆk. Find the work done
View SolutionLet →a=2→i+3→j+4→kand→b=3→i+4→j+5→k. Find the angle between them.
View SolutionA unit vector coplanar with →i+→j+2→kand→i+2→j+→k and perpendicular to →i+→j+→k is _______
View SolutionWrite the unit vector in the direction of →A=5→i+→j−2→k.
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
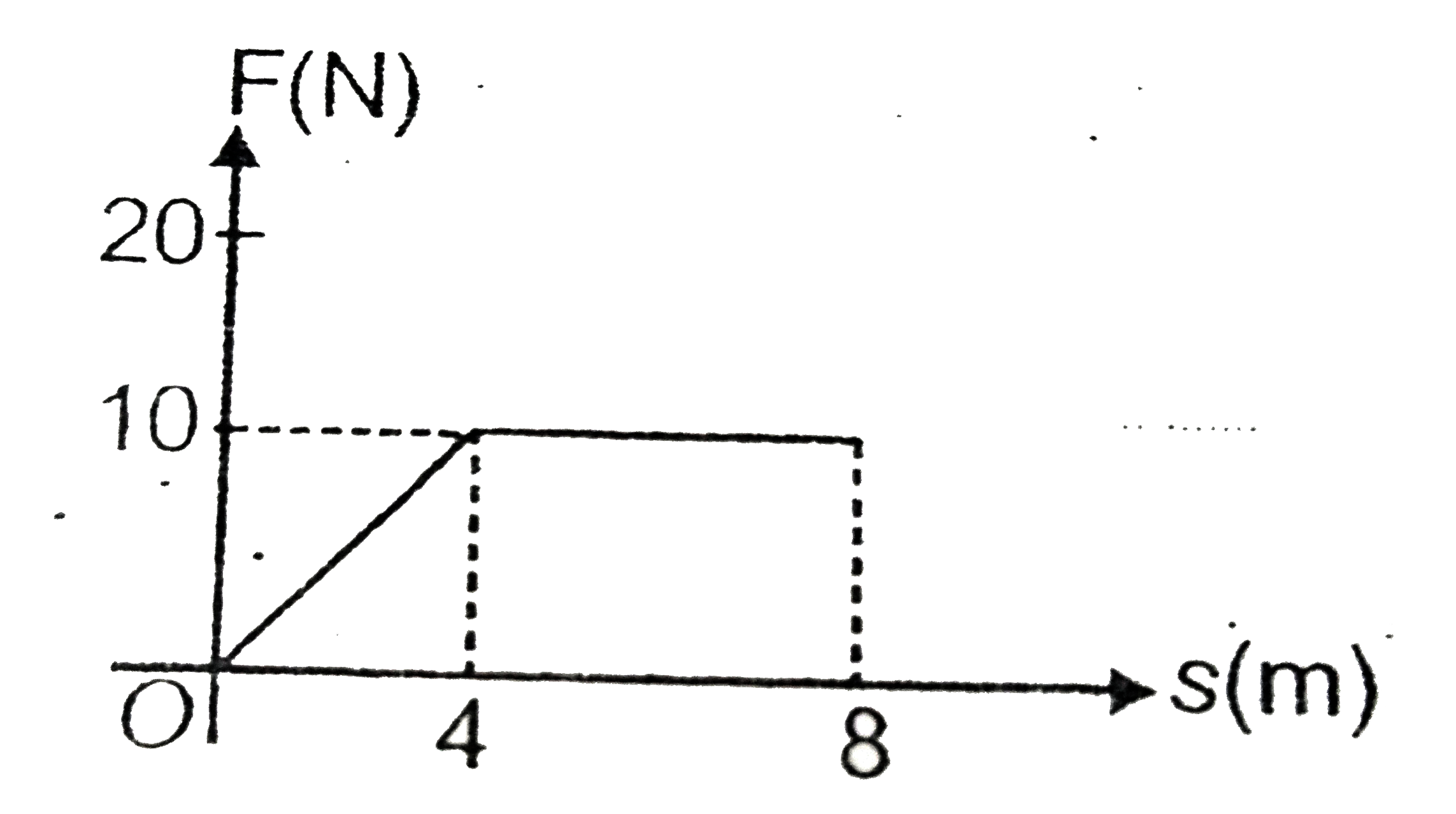
View SolutionFind the equation of the plane through the point 2→i+3→j−→k and perpendicular to the vector 3→i−4→j+7→k.
View Solution
