The correct Answer is:a→r;b→p;c→s;d→q
a. if →a,→band→c are mutaully perpendicular , then
[→a×→b,→b×→c,→c×→a]=[→a→b→c]2
(|→a|∣∣→b∣∣|→c|)2=16
b. Given →aand→b are two unit vectors, i.e., |→a|=∣∣→b∣∣=1 and angle between then is π/3
sinθ=∣∣→a×→b∣∣|→a|∣∣→b∣∣⇒sinπ3=∣∣→a×→b∣∣
√32∣∣→a×→b∣∣
Now
[→a→b+→a×→b→b]=[→a→b→b]+[→a→a×→b→b]
=0+[→a→a×→b→b]
=(→a×→b).(→b×→a)
−(→a×→b).(→a×→b)
−∣∣→a×→b∣∣2
−34
c. if →band→c are othogonal →b.→c=0
Also, if is given that →b×→c=→a Now,
[→a+→b+→c→a+→b→b+→c]
[→a→a+→b→b+→c]+[→b+→c→a+→b→b+→c]
[→a→b→c]
=→a.(→b×→c)
→a.→a=|→a|2=1 ( because →a is a unit vector)
d. [→x→y→a]=0
Therefore, →x,→yand→a are coplanar,
[→x→y→b]=0
Therefore, →x,→yand→b are coplanar,
Also , [→a→b→c]=0
Therefore, →a,→band→c are coplanar,
From (i), (ii) and (iii) ,
→x,→yand→c are coplanar, therefore,
[→x→y→c]=0
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Integer type
17 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Subjective type
19 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Comprehension type
27 Videos
- DETERMINANTSBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions
264 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type
5 Videos
Similar Questions
If →aand→b are any two unit vectors, then find the greatest postive integer in the range of 3∣∣→a+→b∣∣2+2∣∣→a−→b∣∣
View Solutionfrom a point O inside a triangle ABC, perpendiculars, OD, OE and OF are drawn to the sides, BC, CA and AB respectively , prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent.
View SolutionLet →u,→vand→w be three unit vectors such that →u+→v+→w=→a,→u×(→v×→w)=→b,(→u×→v)×→w=→c,→a.→u=3/2,→a.→v=7/4and|→a|=2
Vector →wis
View SolutionProve that |cosα−cosβ|≤|α−β|
View SolutionMatch the following lists:

View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
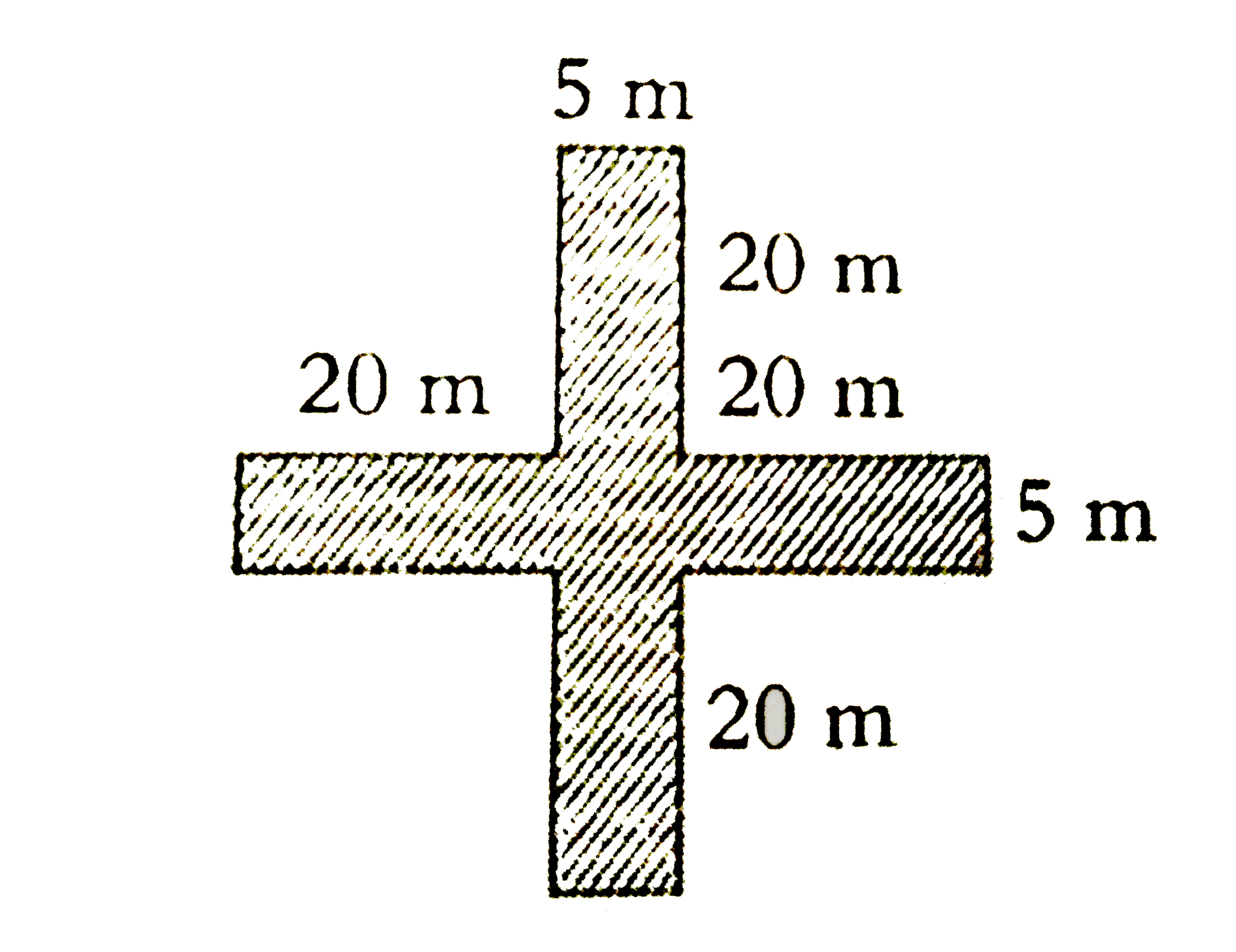
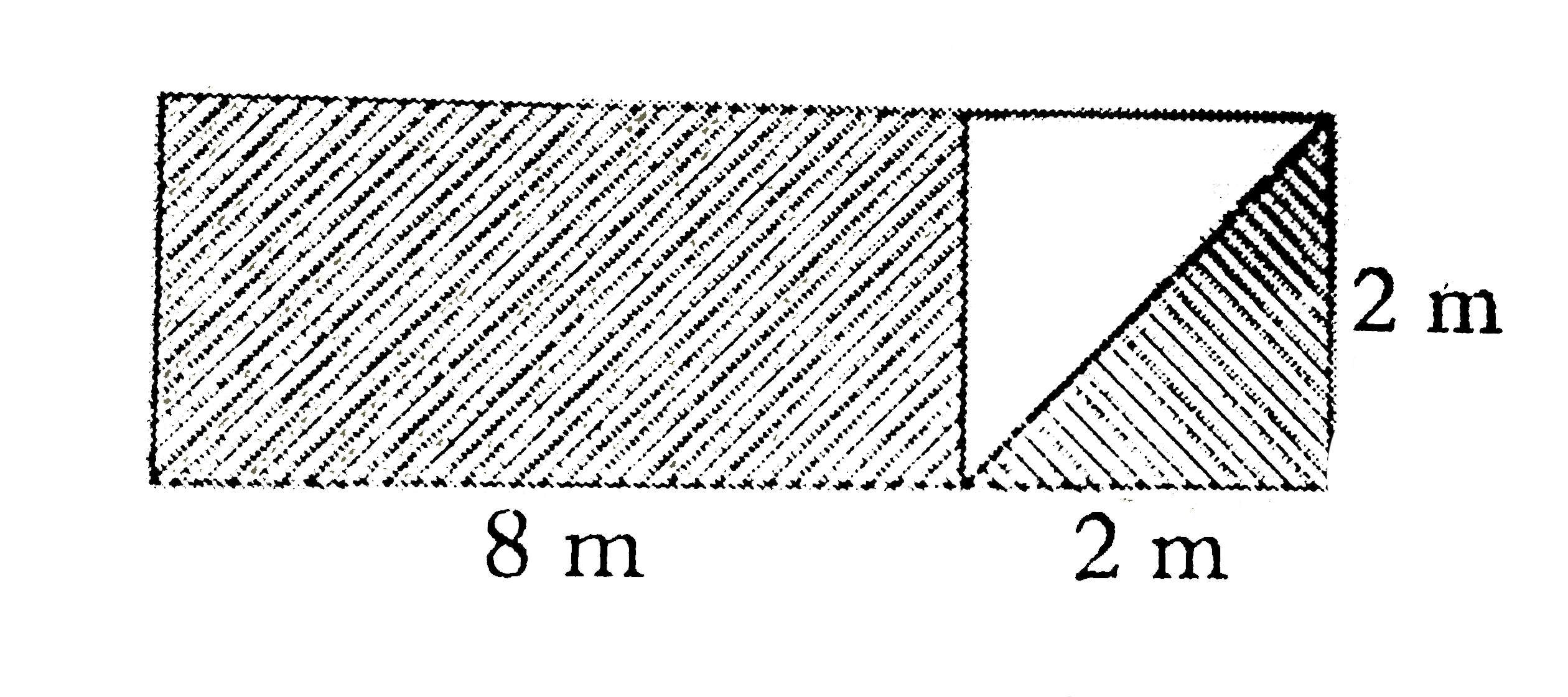
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

