Find the lengths of chords of the circumcircle of triangle ABC, made by its altitudes__________
 From the figure, in ΔABL,
From the figure, in ΔABL,
∠ABL=∠ABD+∠DBL
=B+(90∘−C)
90∘+(B−C)
AL=x
using sine rule in ΔABL, we get xsin(90∘+B−C)=2R
x=2Rcos(B−C)
Similarly, y=2Rcos(C−A)
z=2Rcos(A−B)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.28videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
In the given figure , ABC is a triangle in which ∠BAC=30∘ . Show that BC is equal to the radius of the circumcircle of the traiangle ABC , whose centre is O.
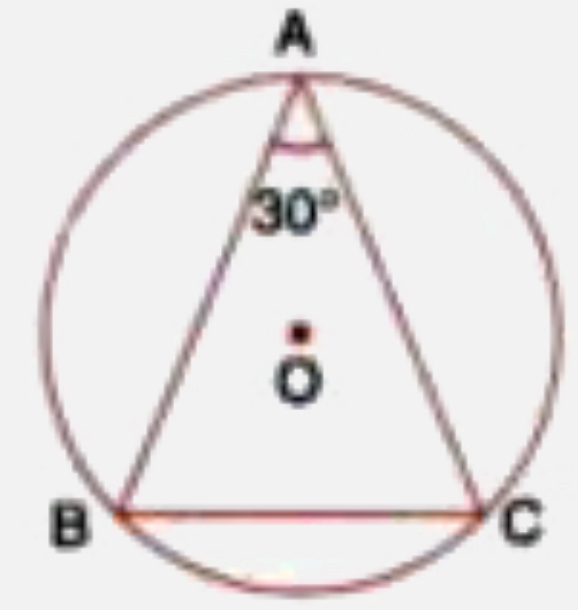 View Solution
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:
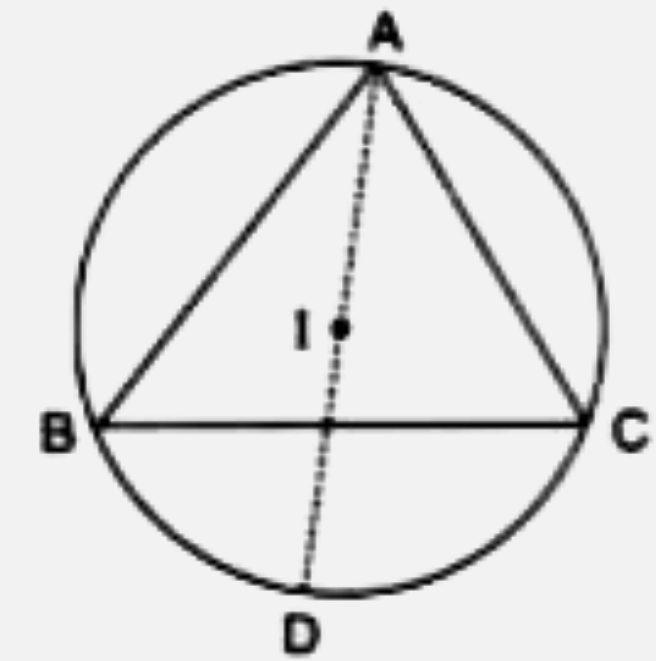
∠DCIView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠BICView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠BCDView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠CBDView SolutionIn a triangle with one angle 2π3, the lengths of the sides form an A.P. If the length of the greatest side is 7 cm, the radius of the circumcircle of the triangle is
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal toView SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If BC=6,AC=8, then the length of side AB is equal toView SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A <br>If ∠GAC=π3anda=3b, then sin C is equal to
View SolutionIf the radius of the circumcircle of the isosceles triangle ABC is equal to AB(=AC), then the angle A is equal to-
View Solution

