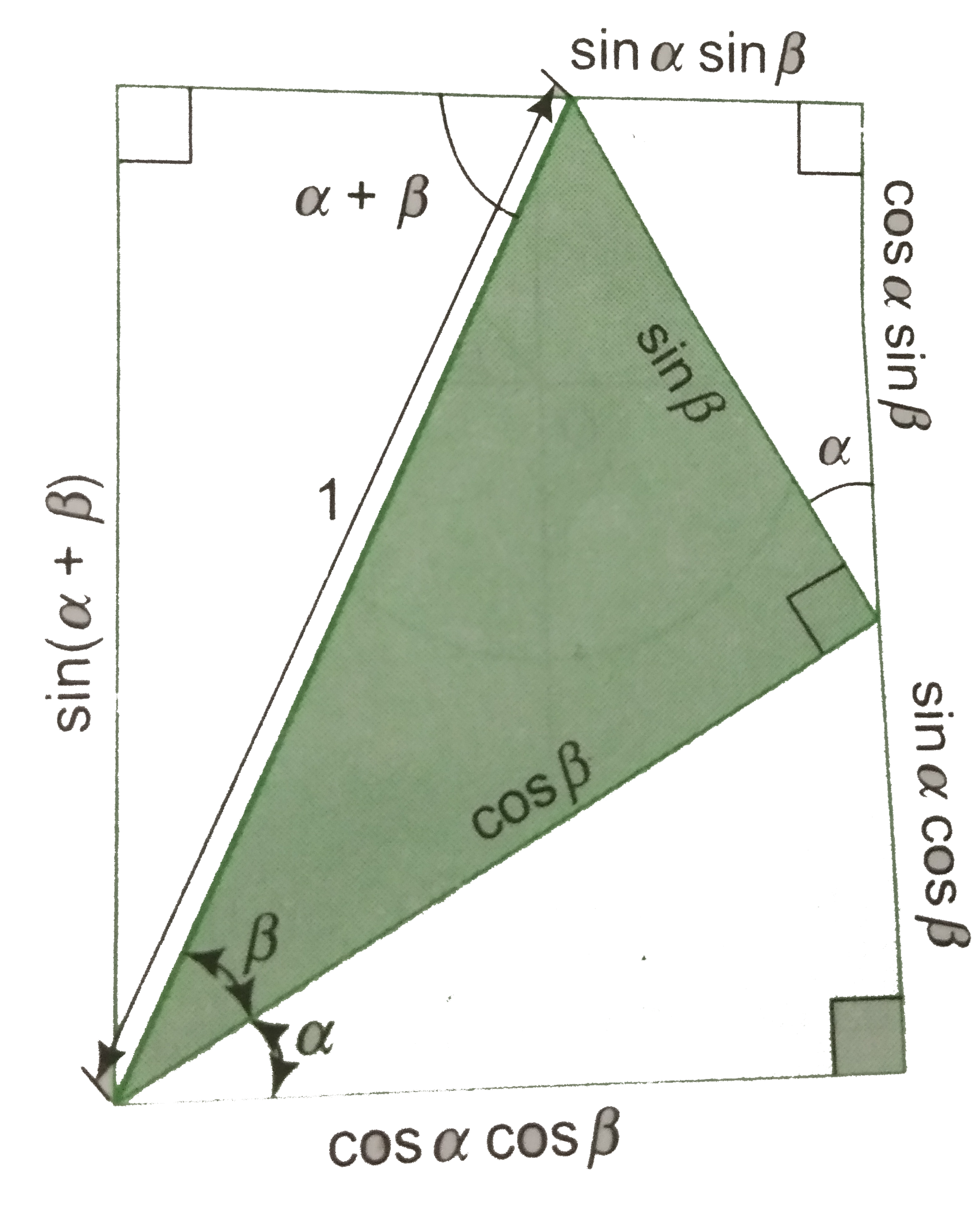
By geometrical interpretation, prove that sin(α+β)s∈αcosβ+sinβcosα cos(α+β)=cosαcosβ−sinαsinβ
Video Solution
Text Solution
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example10videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.18videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
By geometrical interpretation, prove that
(i) sin(α+β)=sinαcosβ+sinβcosα
(ii) cos(α+β)=cosαcosβ−sinαsinβView SolutionBy geometrical interpretation, prove that
tan(α+β)=tanα+tanβ1−tanαtanβ.View SolutionProve that 2sin2β+4cos(α+β)sinαsinβ+cos2(α+β)=cos2α
View Solutionf(α,β)=cos2(α)+cos2(α+β)−2cosαcosβcos(α+β) is
View SolutionProve that : cos2α+cos2(α+β)−2cosαcosβcos(α+β)=sin2β
View SolutionProve that (sinαcosβ+cosαsinβ)2+(cosαcoaβ−sinαsinβ)2=1.
View SolutionProve by vector methods that sin(α+β)=sinαcosβ+cosαsinβ
View SolutionProve that: cos2α cos2β+sin2(α−β)−sin2(α+β)=cos2(α+β) .
View SolutionSimplify 2sin2β+4cos(α+β)sinαsinβ+cos2(α+β)
View SolutionShow that: sin2α+sin2β+2sinαsinβcos(α+β)=sin2(α+β)
View Solution