Question

Find the reference angle $\theta \text{'}$for the following angles in standerd position : (a)$\theta ={300}^{\circ }\text{(b)}\theta =2.3\text{(c )}\theta =-{135}^{\circ }$

Answer

(a) `60^@" (b) "0.8416" (c ) " 45^@`

Explanation

(a)
Because `300^@` lies in Quadrant IV, the acute angle it makes with the x-axis is `theta'=360^@-300^@=60^@`
)(b)
Because 2.3 lies between `pi//2~~1.5708" and "pi~~3.1416`, it follows that it is in Quadrant II and its reference angle is `theta'=pi-2.3~~0.8416`.
(c )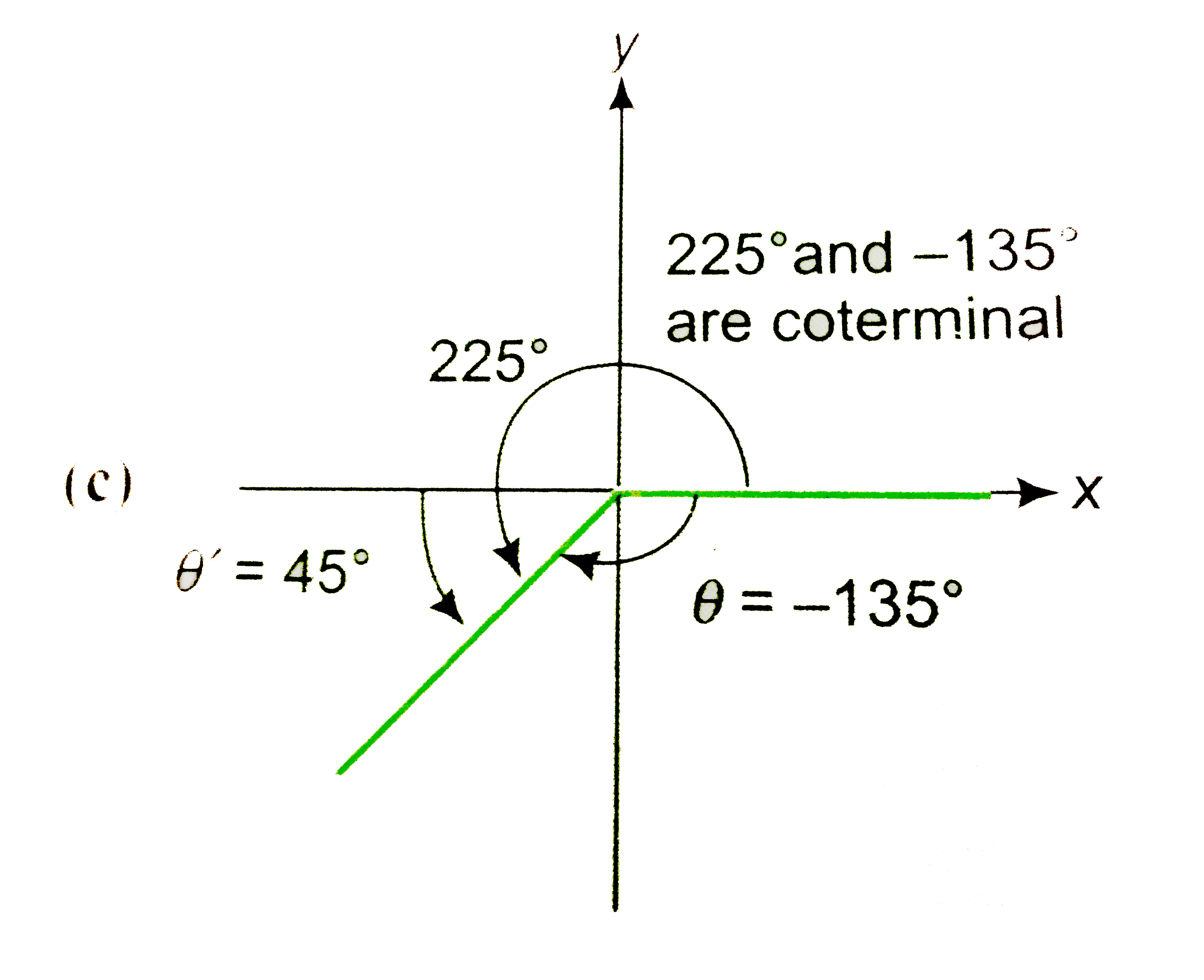
First, determine that`-135^@` is coterminal with `225^@`, which lies in Quadrant III. So, the reference angle is `theta'=225^@-180^@=45^@`.