α,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
Which of the following holds?
cos(α−δ)>0
cos(α−δ)=0
cos(α−δ)<0
cos(α−δ)>0orcos(α−δ)<0
The correct Answer is:A
To solve the problem, we need to analyze the angles α, β, γ, and δ, which are in the first, second, third, and fourth quadrants respectively, and they form an increasing arithmetic progression (AP).
1. Understanding Quadrants:
- α is in the first quadrant: 0<α<π2
- β is in the second quadrant: π2<β<π
- γ is in the third quadrant: π<γ<3π2
- δ is in the fourth quadrant: 3π2<δ<2π
2. Arithmetic Progression:
Since α, β, γ, and δ are in an increasing AP, we can express them in terms of a common difference d:
- β = α + d
- γ = α + 2d
- δ = α + 3d
3. Establishing Inequalities:
From the definitions of the quadrants, we can establish the following inequalities:
- For β: π2<α+d<π
- For γ: π<α+2d<3π2
- For δ: 3π2<α+3d<2π
4. Finding Relationships:
From the inequality for β:
d>π2−α(1)
From the inequality for γ:
2d>π−α⇒d>π−α2(2)
From the inequality for δ:
3d>3π2−α⇒d>3π2−α3(3)
5. Combining Inequalities:
Now we need to analyze these inequalities to find a consistent value for d. Since d must satisfy all three inequalities, we can set up a relationship:
- From (1) and (2):
π2−α<π−α2⇒π−2α<π2⇒2α>π2⇒α>π4
6. Conclusion:
Since α is in the first quadrant, and we've established that α>π4, we can conclude that:
- cos(α)>0
- cos(β)>0
- cos(γ)<0
- cos(δ)>0
Therefore, the cosine of the differences:
- cos(α−γ) and cos(α−δ) will both be greater than 0, confirming that the correct option is that they are greater than or equal to 0.
Final Answer
The correct statement is that cos(α−γ)>0 and cos(α−δ)>0.
- α is in the first quadrant: 0<α<π2
- β is in the second quadrant: π2<β<π
- γ is in the third quadrant: π<γ<3π2
- δ is in the fourth quadrant: 3π2<δ<2π
Since α, β, γ, and δ are in an increasing AP, we can express them in terms of a common difference d:
- β = α + d
- γ = α + 2d
- δ = α + 3d
From the definitions of the quadrants, we can establish the following inequalities:
- For β: π2<α+d<π
- For γ: π<α+2d<3π2
- For δ: 3π2<α+3d<2π
From the inequality for β:
d>π2−α(1)
From the inequality for γ:
2d>π−α⇒d>π−α2(2)
From the inequality for δ:
3d>3π2−α⇒d>3π2−α3(3)
Now we need to analyze these inequalities to find a consistent value for d. Since d must satisfy all three inequalities, we can set up a relationship:
- From (1) and (2):
π2−α<π−α2⇒π−2α<π2⇒2α>π2⇒α>π4
Since α is in the first quadrant, and we've established that α>π4, we can conclude that:
- cos(α)>0
- cos(β)>0
- cos(γ)<0
- cos(δ)>0
- cos(α−γ) and cos(α−δ) will both be greater than 0, confirming that the correct option is that they are greater than or equal to 0.
The correct statement is that cos(α−γ)>0 and cos(α−δ)>0.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Matrix Match Type3videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Numerical Value Type11videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Correct Answers Type17videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
α,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
Which of the following does not hold?View Solutionα,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
if α+β+γ+δ=θandα70∘, thenView Solution
Knowledge Check
- Question 1 - Select One
Line l in the xy-plane contains points from each of Quadrants II, III, and IV, but no points from Quadrant I. Which of the following must be true?
AThe slope of line l is undefined.BThe slope of line l is zero.CThe slope of line l is positive.DThe slope of line l is negative.
In a arithmetic progression whose first term is α and common difference is β,α,β≠0 the ratio r of the sum of the first n terms to the sum of n terms succeending them, does not depend on n. Then which of the following is /are correct ?
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
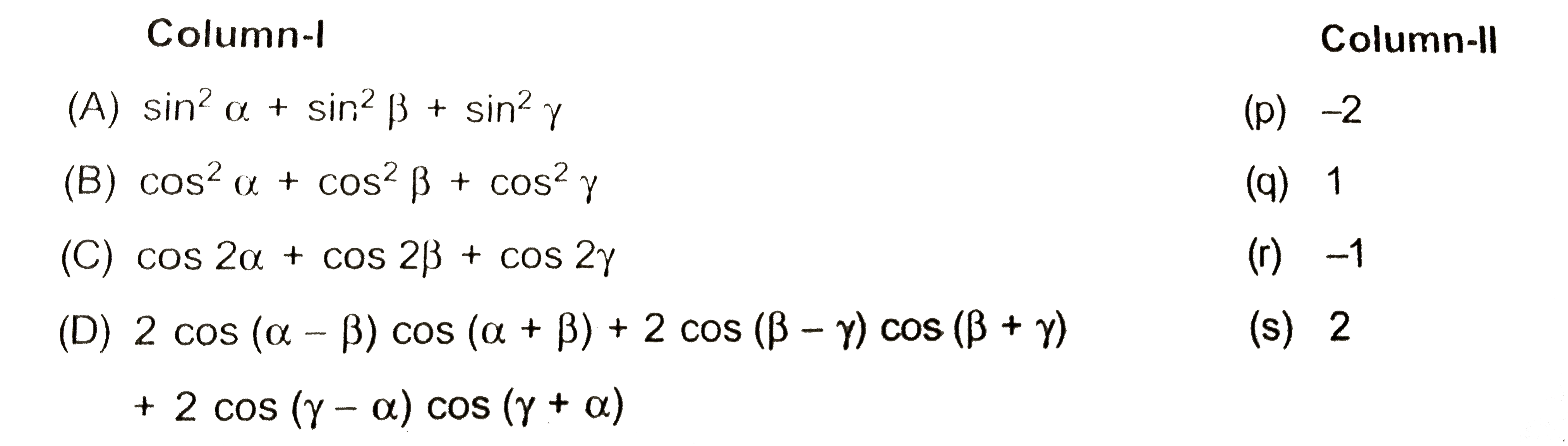 View Solution
View SolutionFind the intervals in which f(x) = sin 3x, x∈[0,π2] is (i) increasing, (ii) decreasing.
View SolutionThe frquencies of Kα,Kβ and Lα X-rays of a materail are γ1,γ2andγ3 respectively. Which of the following relation holds good?
View SolutionFind the intervals in which the following functions are:
(i) increasing
.(ii)decreasing f(x)=2x2−6x
View SolutionConsider angles α=(2n+12)π±A and β=mπ+(−1)m(π2−A) where n, m ∈ I. Which of the following is not true ?
View SolutionLet α,βandγ be some angles in the first quadrant satisfying tan(α+β)=158andcosecγ=178, then which of the following hold(s) good? (a) α+β+γ=π (b)cotα+cotβ+cotγ=cotαcotβcotγ (c)tanα+tanβ+tanγ=tanαtanβtanγ (d)tanαtanβ+tanβtanγ+tanγtanα=1
View Solution

