The solution of ∣∣∣x+1x∣∣∣>2 is
A
R−{0}
B
R−{−1,0,1}
C
R−{1}
D
R−{−1,1}
Video Solution
Text Solution
The correct Answer is:B
To solve the inequality |x+1x|>2, we will follow these steps:
Step 1: Analyze the expression
The expression inside the modulus is x+1x. We need to ensure that x≠0 since division by zero is undefined.
The expression inside the modulus is x+1x. We need to ensure that x≠0 since division by zero is undefined.
|
Updated on:7/8/2024
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type2videos
INDEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Jee Advanced (Single1videos
INEQUALITIES INVOLVING MEANS
Similar Questions
Knowledge Check
- Question 1 - Select One
The solution set of |x−1|x>2 is
A0<x<13Bx<13Cx>13D13<x<1 - Question 2 - Select One
If x is a negative integar , then the solution set of −12x>30 is
AA. {−2,−1}BB. {…,−5,−4,−3}CC. {…,−5,−4,−3,−2}DD. {−2,−1,0,1,2…} - Question 3 - Select One
The solution set of 1≥15−7x>2x−27,x∈N on the number line is
A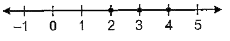 B
B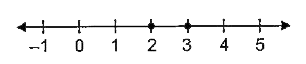 C
C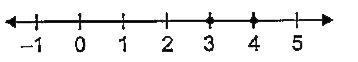 D
D
The solution of 6+x−x2>0, is
View SolutionThe solution set of the inequation ∣∣∣3x+1∣∣∣>2, is
View SolutionWhich of the following is not the solution logx(52−1x)>(52−1x) ?
View SolutionThe solution set of the inequation x−1x−2>2, is
View SolutionIf x∈W, find the solution set of 35x−2x−13>1.
View Solution

