Find the number of ways of arranging 15 students A1,A2,........A15 in a row such that (i) A2, must be seated after A1andA2, must come after A2 (ii) neither A2 nor A3 seated brfore A1
2!×15!3!
15!3!
2!15!
None of these
The correct Answer is:A
To solve the problem of arranging 15 students A1,A2,…,A15 under the given conditions, we will break it down into two parts as specified in the question.
Part (i): Arranging with conditions A2 must be seated after A1 and A3 must come after A2.
1. Choose Seats for A1,A2,A3:
We need to select 3 seats out of the 15 for A1,A2, and A3. The number of ways to choose 3 seats from 15 is given by the combination formula:
(153)
2. Arrange A1,A2,A3:
Since A1 must come before A2, and A2 must come before A3, there is only 1 way to arrange them in the chosen seats:
1 way
3. Arrange Remaining Students:
After placing A1,A2, and A3, we have 12 students left to arrange in the remaining 12 seats. The number of ways to arrange these 12 students is:
12!
4. Total Arrangements for Part (i):
The total number of arrangements for part (i) is:
Total=(153)×1×12!=(153)×12!
Part (ii): Neither A2 nor A3 seated before A1.
1. Choose Seats for A1,A2,A3:
Again, we choose 3 seats from 15 for A1,A2, and A3:
(153)
2. Arrange A1,A2,A3:
Here, A1 must be seated before both A2 and A3. There are 2 valid arrangements for A2 and A3 after A1:
- A1,A2,A3
- A1,A3,A2
Thus, there are:
2 ways
3. Arrange Remaining Students:
The remaining 12 students can still be arranged in the remaining 12 seats:
12!
4. Total Arrangements for Part (ii):
The total number of arrangements for part (ii) is:
Total=(153)×2×12!
Final Answers:
- For part (i): (153)×12!
- For part (ii): (153)×2×12!
We need to select 3 seats out of the 15 for A1,A2, and A3. The number of ways to choose 3 seats from 15 is given by the combination formula:
(153)
Since A1 must come before A2, and A2 must come before A3, there is only 1 way to arrange them in the chosen seats:
1 way
After placing A1,A2, and A3, we have 12 students left to arrange in the remaining 12 seats. The number of ways to arrange these 12 students is:
12!
The total number of arrangements for part (i) is:
Total=(153)×1×12!=(153)×12!
Again, we choose 3 seats from 15 for A1,A2, and A3:
(153)
Here, A1 must be seated before both A2 and A3. There are 2 valid arrangements for A2 and A3 after A1:
- A1,A2,A3
- A1,A3,A2
2 ways
The remaining 12 students can still be arranged in the remaining 12 seats:
12!
The total number of arrangements for part (ii) is:
Total=(153)×2×12!
- For part (i): (153)×12!
- For part (ii): (153)×2×12!
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Multiple Correct Answer2videos
PERMUTATION AND COMBINATION
- BOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension8videos
PERMUTATION AND COMBINATION
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Matching Column Type1videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Sovled Examples22videos
PRINCIPLE OF MATHEMATICAL INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
IfA1andA2 are two AMs between a and b then (2A1−A2)(2A2−A1)=
AabBbaCbaDa2b
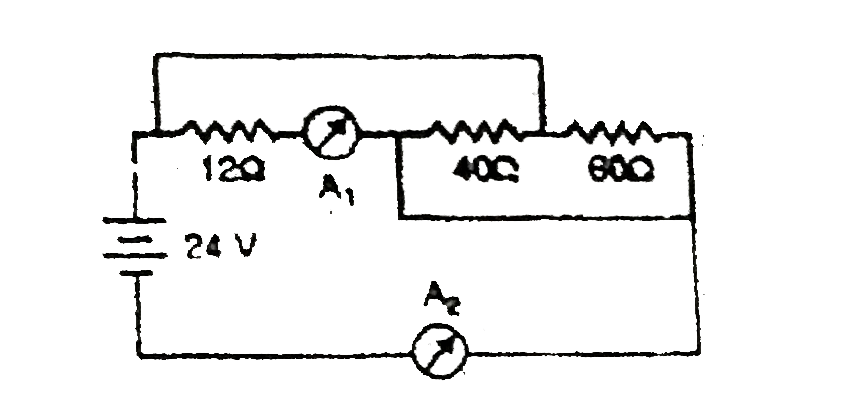
In the following circuit readings in ammeters A1 and A2 will be -
 View Solution
View SolutionIn the circuit of figure A1 and A2 are ideal ammeters. Then the reading in ammeter A2 is
 View Solution
View SolutionIf A1,A2,A3,..are sets such that n(Ai)=101−i, A1⊃A2⊃A3⊃...⊃A100 and A=∩100i=5Ai then n(A) is equal to
View SolutionFind the sum of first 24 terms of the A.P. a1,a2,a3......., if it is inown that a1+a5+a10+a15+a20+a24=225.
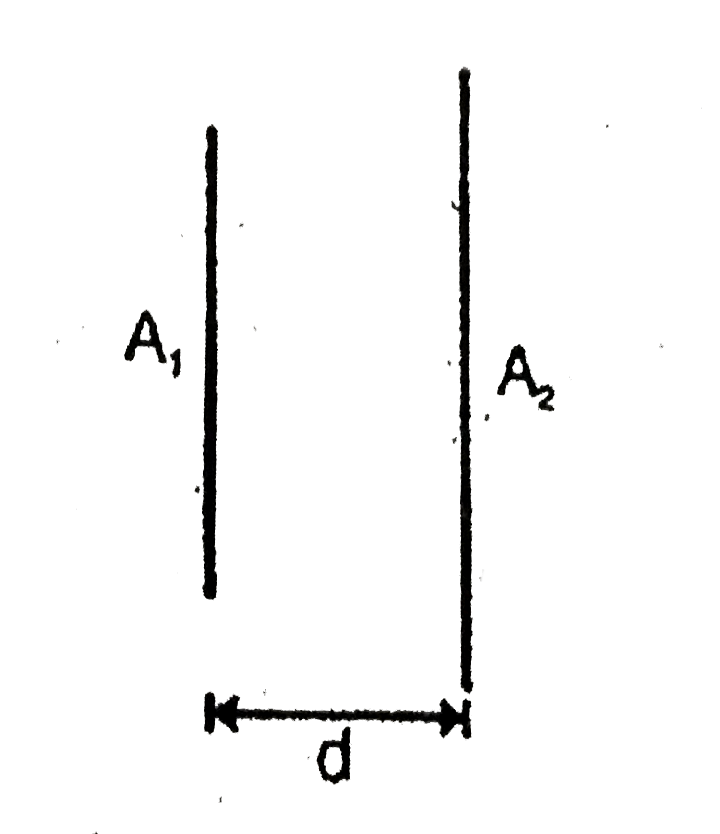
View SolutionThe capacitance of capacitor of plate areas A1 and A2 (A1<A2 at a distance d is
 View Solution
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
 View Solution
View Solutionif A1,A2,A3,....A100are set of A1⊃A2⊃A3⊃A4.....⊃A100 n(Ai)=i+2 , ∩100i=3Ai =
View Solution

