If either of the two P, Q and R are equal and P+Q+R=180∘, then the value of ∣∣ ∣ ∣∣11+sinPsinP(1+sinP)11+sinQsinQ(1+sinQ)11+sinRsinR(1+sinR)∣∣ ∣ ∣∣ is
0
1
sin(P+Q+R)
sinΨnQsinR
The correct Answer is:A
To solve the problem, we need to find the value of the determinant given the angles P, Q, and R such that P+Q+R=180∘ and at least two of the angles are equal.
The determinant we need to evaluate is:
D=∣∣
∣
∣∣11+sinPsinP(1+sinP)11+sinQsinQ(1+sinQ)11+sinRsinR(1+sinR)∣∣
∣
∣∣
Step 1: Subtract Column 1 from Column 2
We will perform the operation C2→C2−C1:
D=∣∣
∣
∣∣1sinPsinP(1+sinP)1sinQsinQ(1+sinQ)1sinRsinR(1+sinR)∣∣
∣
∣∣
Step 2: Subtract Column 2 from Column 3
Next, we perform the operation C3→C3−C2:
D=∣∣
∣
∣∣1sinPsinP21sinQsinQ21sinRsinR2∣∣
∣
∣∣
Step 3: Apply Row Operations
Now, we will apply row operations to simplify the determinant. We can subtract Row 1 from Rows 2 and 3:
D=∣∣
∣
∣∣1sinPsinP20sinQ−sinPsinQ2−sinP20sinR−sinPsinR2−sinP2∣∣
∣
∣∣
Step 4: Factor the Determinant
Now we can factor the determinant:
D=∣∣
∣
∣∣1sinPsinP20sinQ−sinP(sinQ−sinP)(sinQ+sinP)0sinR−sinP(sinR−sinP)(sinR+sinP)∣∣
∣
∣∣
Step 5: Expand the Determinant
The determinant simplifies to:
D=(sinQ−sinP)(sinR−sinP)⋅∣∣∣1sinP1sinR+sinP∣∣∣
Step 6: Calculate the 2x2 Determinant
Calculating the 2x2 determinant:
∣∣∣1sinP1sinR+sinP∣∣∣=1(sinR+sinP)−1(sinP)=sinR
Step 7: Final Expression for the Determinant
Thus, we have:
D=(sinQ−sinP)(sinR−sinP)⋅sinR
Step 8: Evaluate the Determinant
Since we know that at least two angles among P, Q, and R are equal, this means that either sinQ=sinP or sinR=sinP. Therefore, at least one of the factors in the product will be zero, leading to:
D=0
Conclusion
The value of the determinant is 0.
∣
∣∣11+sinPsinP(1+sinP)11+sinQsinQ(1+sinQ)11+sinRsinR(1+sinR)∣∣
∣
∣∣
∣
∣∣1sinPsinP(1+sinP)1sinQsinQ(1+sinQ)1sinRsinR(1+sinR)∣∣
∣
∣∣
∣
∣∣1sinPsinP21sinQsinQ21sinRsinR2∣∣
∣
∣∣
∣
∣∣1sinPsinP20sinQ−sinPsinQ2−sinP20sinR−sinPsinR2−sinP2∣∣
∣
∣∣
∣
∣∣1sinPsinP20sinQ−sinP(sinQ−sinP)(sinQ+sinP)0sinR−sinP(sinR−sinP)(sinR+sinP)∣∣
∣
∣∣
Topper's Solved these Questions
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Comprehension
2 Videos
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE ADVANCED
38 Videos
- DETERMINANTSBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions
264 Videos
Similar Questions
If P,Q and R are the angles of a triangle the value of ∣∣ ∣ ∣∣tanP111tanQ111tanR∣∣ ∣ ∣∣ is
View SolutionIf the points P(1,5), Q(−1,1) and R(4,y) are collinear, find the value of y.
View SolutionIf P=(1,1),Q=(3,2) and R is a point on x-axis then the value of PR+RQ will be minimum at
View SolutionIn △PQR , right angled at Q, PQ=4cm and RQ=3cm . Find the values of sinP , sinR , secP and secR .
View SolutionIn DelatOPQ , right - angled at P , OP = 7 cm and OQ - PQ =1 cm . Determine the values of sinQ and cos Q .
View SolutionIn △OPQ right angled at P, OP=7cm , OQ−PQ=1cm . Determine the values of sinQ and cosQ .
View SolutionIf p is nearly equal to q and n > 1 , such that
(n+1)p+(n−1)q(n−1)p+(n+1)q=(pq)k , then the value of k, is
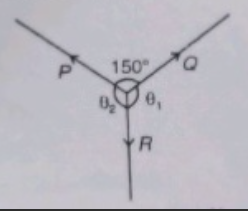
View SolutionP,Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1N , sinθ1=12 , the value of R is
View SolutionIn a ΔPQR. if 3sinP+4cosQ=6 and 4sinQ+3cosP=1, then the angle R is equal to:
View SolutionIfp>q>0andpr<−1<qr, then find the value of tan−1(p−q1+pq)+tan−1(q−r1+qr)+tan−1(r−p1+rp).
View Solution
