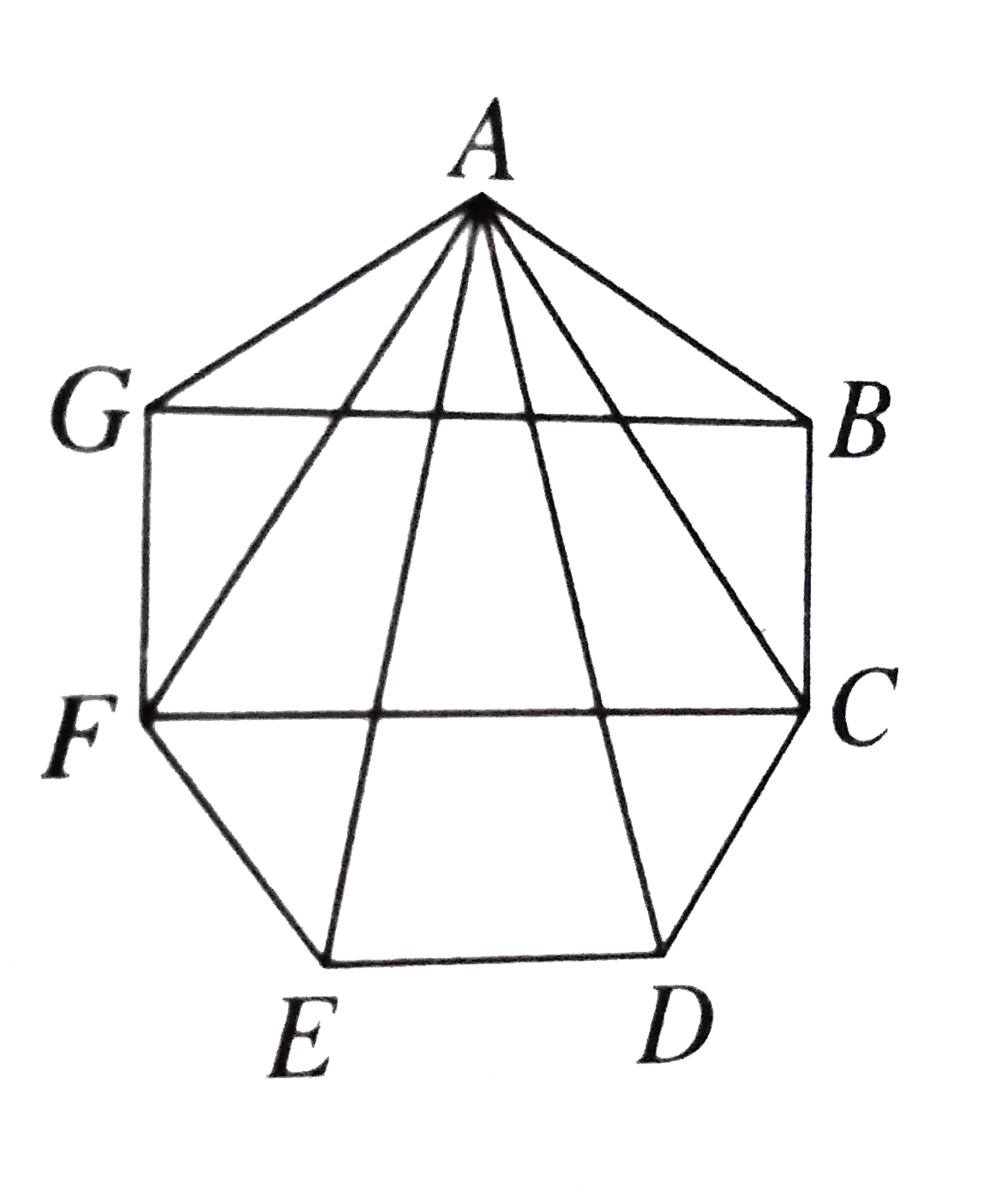
Three vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they form the vertices of an isosceles triangle is
17
13
37
35
The correct Answer is:D
(d) ΔAGB, ΔAFC and ΔAED are isosceles
∴P=7C1×3'7C3=7×37×6×53×2=35
Topper's Solved these Questions
- PROBABILITYBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITYEXERCISE - Multiple Correct Answer
13 Videos
- PROBABILITYBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITYEXERCISE - Comprehension
2 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Sovled Examples
22 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
Similar Questions
Three vertices are chosen at random from the vertices of a regular hexagon then
The probability that the triangle has exactly two sides common with the side of the hexagon is
View SolutionThree of the six vertices of a regular hexagon are chosen the random. What is the probability that the triangle with these vertices is equilateral.
View Solution
Knowledge Check
Three of six vertices of a regular hexagon are chosen at random. Tie probability that the triangle formed by these vertices is an equilateral triangle is
A320B310C−110D14
The locus of vertices of all isosceles triangles having a common base.
View SolutionCheck whether (5,−2),(6,4)and(7,−2) are the vertices of an isosceles triangle.
View SolutionIf the lengths of the sides of a triangle are decided by the three thrown of a single fair die,then the probability that the triangle is of maximum area given that it is an isosceles triangle, is
View SolutionIf four vertices a regular octagon are chosen at random, then the probability that the quadrilateral formed by them is a rectangle is
View SolutionThree of six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral is (a) 12 (b) 15 (c) 110 (d) 120
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionProve that the points (5, -2), (-4, 3) and (10, 7) are the vertices of an isosceles right-angled triangle.
View Solution
