Solve x−2x+2>2x−34x−1.
Video Solution
Text Solution
x−2x+2>2x−34x−1
or (x−2)(4x−1)−(x+2)(2x−3)(x+2)(4x−1)>0
or 4x2−9x+2−2x2−x+6(x+2)(4x−1)>0
or x2−5x+4(x+2)(4x−1)>0
or (x−1)(x−4)(x+2)(4x−1)>0
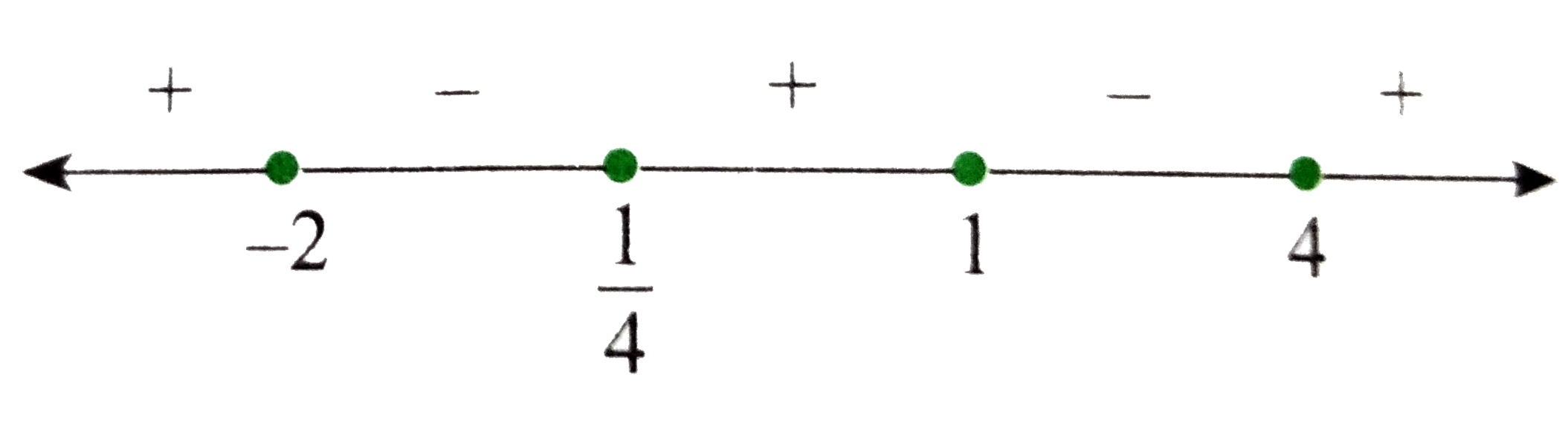
⇒x∈(−∞,−2)∪(14,1)1∪(4,∞)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solved Examples15videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.115videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Solve x−2x+2>2x−34x−1
View SolutionSolve for : x:x−1x−2+x−3x−4=313,x≠2,4
View SolutionSolve for x : x−1x−2+x−3x−4=313; x≠2, 4
View SolutionSolve for x : x−1x+2+x−3x−4=103, x≠−2, 4
View SolutionSolve (i) x−1x−x+1x−1<2 (ii) x2+4x+42x2−x−1>0.
View SolutionSolve x3(2x−1)(x−1)2
View SolutionSolve 2x−3x−1+1=9x−x2−6x−1.
View SolutionSolve 2x−3x−1+1=6x−x2−6x−1.
View SolutionSolve x(x+2)2(x−1)5(2x−3)(x−3)4≥0.
View SolutionSolve x(x+2)2(x−1)5(2x−3)(x−3)4≥0.
View Solution

