Solve: $\frac{| x + 3 | + x}{x + 2} > 1$

Video Solution

Text Solution

Verified by Experts

We have $\frac{| x + 3 | + x}{x + 2} > 1$
Clearly, the L.H.S. of this inequation is meaningful for $x \neq - 2$ .
Given $\frac{| x + 3 | + x}{x + 2} > 1$
or $\frac{| x + 3 | + x}{x + 2} - 1 > 0$
or $\frac{| x + 3 | + x - x - 2}{x + 2} > 0$
or $\frac{| x + 3 | - 2}{x + 2} > 0$
If $| x + 3 | - 2 = 0$ , then $x + 3 = \pm 2 or x = - 5, - 1$ .
Hence, the sign scheme of the expression $\frac{| x + 3 | - 2}{x + 2}$ is as follows :

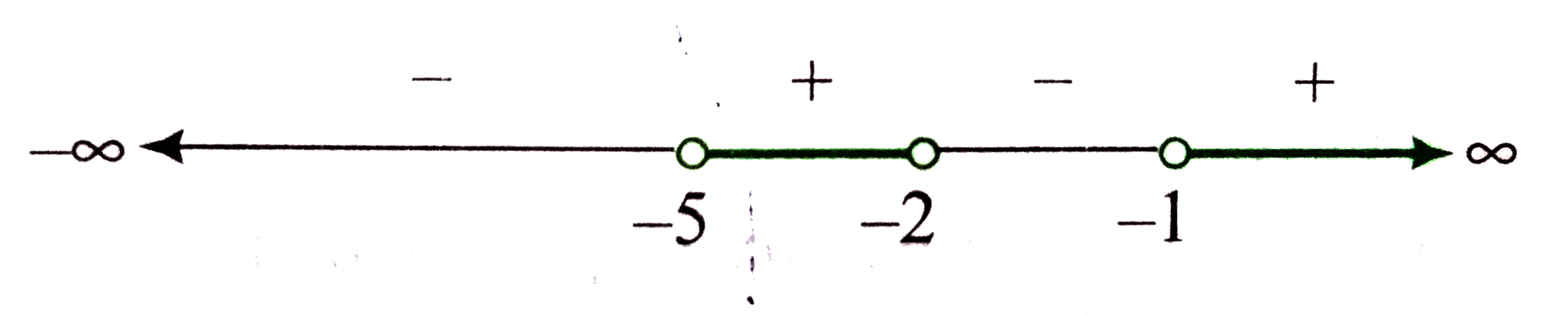
From the above sign scheme, $x \in (- 5, - 2) \cup (- 1, \infty)$ .

|

Updated on:21/07/2023

Class 12 MATHS RELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-RELATIONS AND FUNCTIONS-Archives(Matrix Match Type)

Home
Ask Doubt
Profile