Find domain for f(x)=√cos(sinx)
Video Solution
Text Solution
f(x)=√cos(sinx) is defined if
cos(sinx)≥0
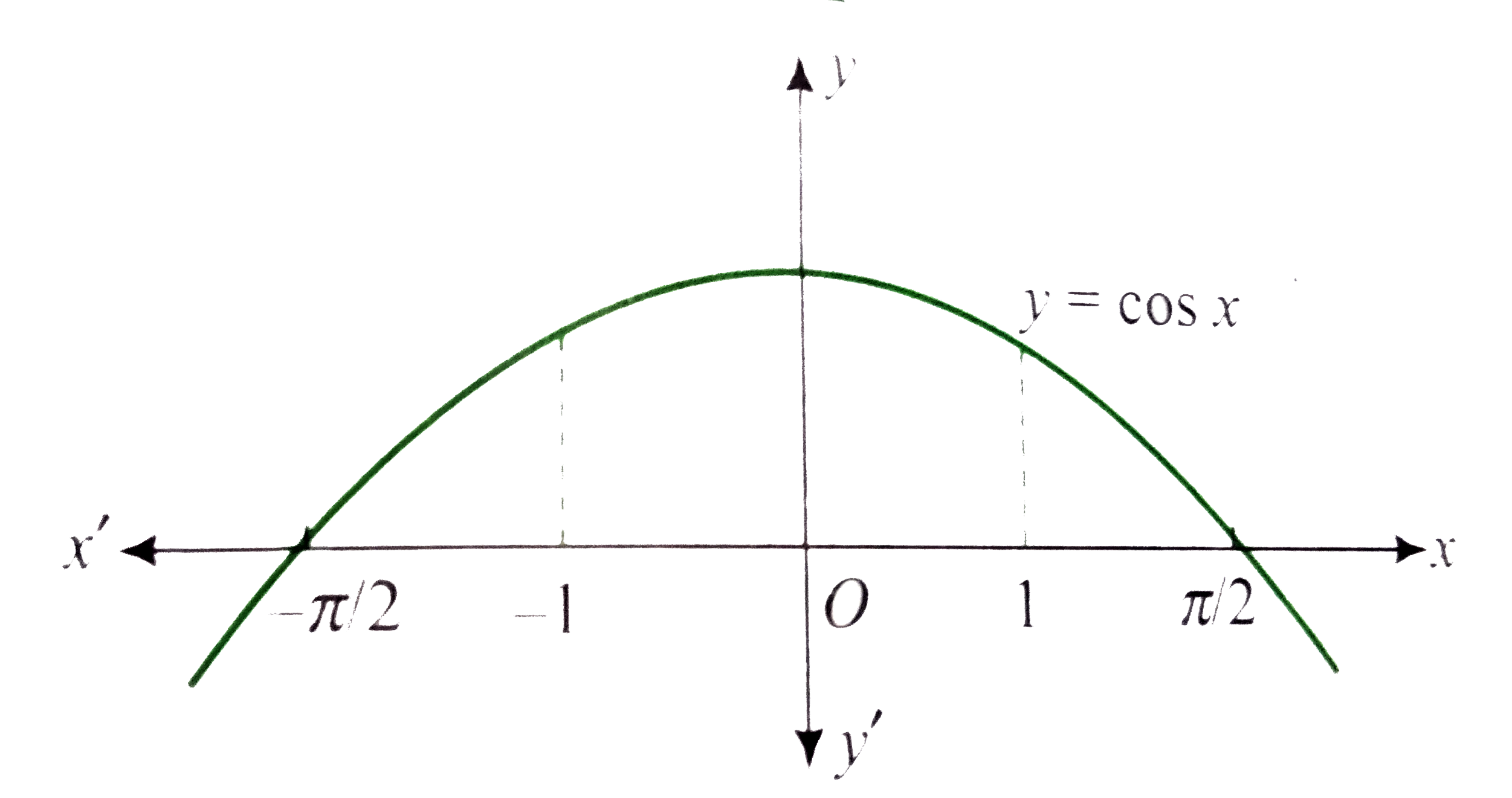
As we know, −1≤sinx≤1 for all x.
So, cosθ≥0
(Here, θ=sinx lies in the first and fourth quadrants)
i.e., cos(sinx)≥0 for all x
i.e., x∈R
Thus, the dimain f(x) is R.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solved Examples15videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.115videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Find the domain of f(x)=√cos−1x−sin−1x
View SolutionFind the domain of f(x)=√cos−1x−sin−1x
View SolutionFind the domain of f(x)=√sinx+√16−x2
View SolutionFind domain for, f(x)=cos−1[x].
View SolutionFind domain for f(x)=[sinx]cos(π[x−1]).
View SolutionFind the domain of f(x)=√([x]−1)+√(4−[x]) (where [ ] represents the greatest integer function).
View SolutionFind the domain of f(x)=1√x+|x|
View SolutionFind the domain of f(x)=1√x−|x|
View SolutionFind the range of f(x)=√sin(cosx)+√cos(sinx).
View SolutionFind the domain of f(x)=√x−11.
View Solution

