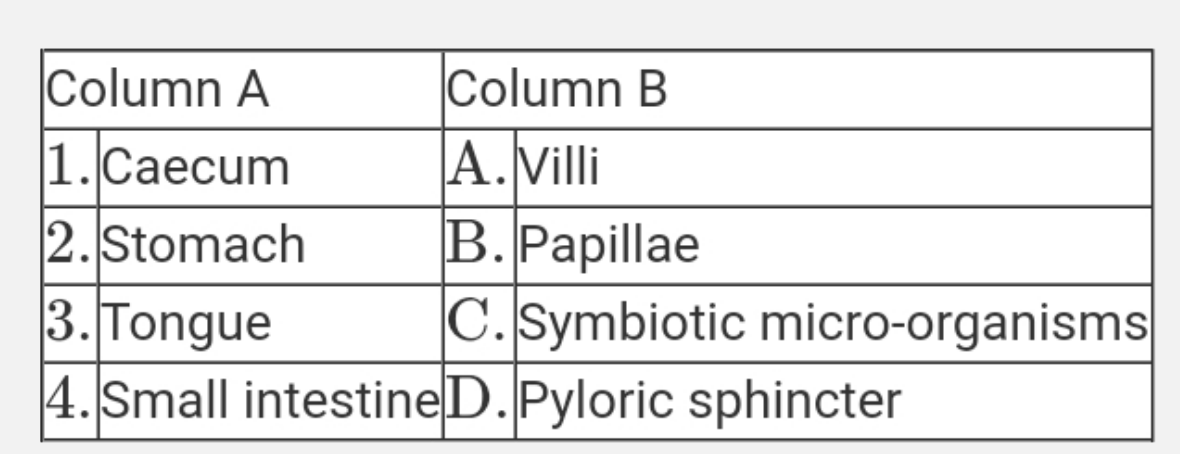
Match the column

Video Solution
Text Solution
The correct Answer is:p→c;q→a;r→c;s→b
(p) f(x)=sin3x+cos4x,
sin3x has period 2π and cos4x has period π, and L.C.M. of π and 2π is 2π. Hence, period is 2π.
(q) f(x)=sin4x+cos4x,
Both sin4x and cos4x have the same period π, and L.C.M. of π and π is π.
But f(x+π/2)=f(x). Then period is π/2.
(r) Both sin3x and cos3x have the same period 2π, and L.C.M. of 2π and 2π is 2π.
Hence, period is 2π,[(f(x+π)≠f(x)].
(s) f(x)=cos4x−sin4x
Both sin4x and cos4x have the same period π, and L.C.M. of π and π is π.
Hence, period is π,[f(x+π/2)≠f(x)].
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.12
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.13
7 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.10
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos