Two vertices of a triangle are (1, 3) and (4, 7). The orthocentre lies on the line x+y=3. The locus of the third vertex is
x2−2xy+2y2−3x−4y+36=0
2x2−4xy+3y2−4x−y+42=0
3x2+xy−4y2−2x+24y−40=0
x2−4xy+3y2−2x−y+40=0
The correct Answer is:C
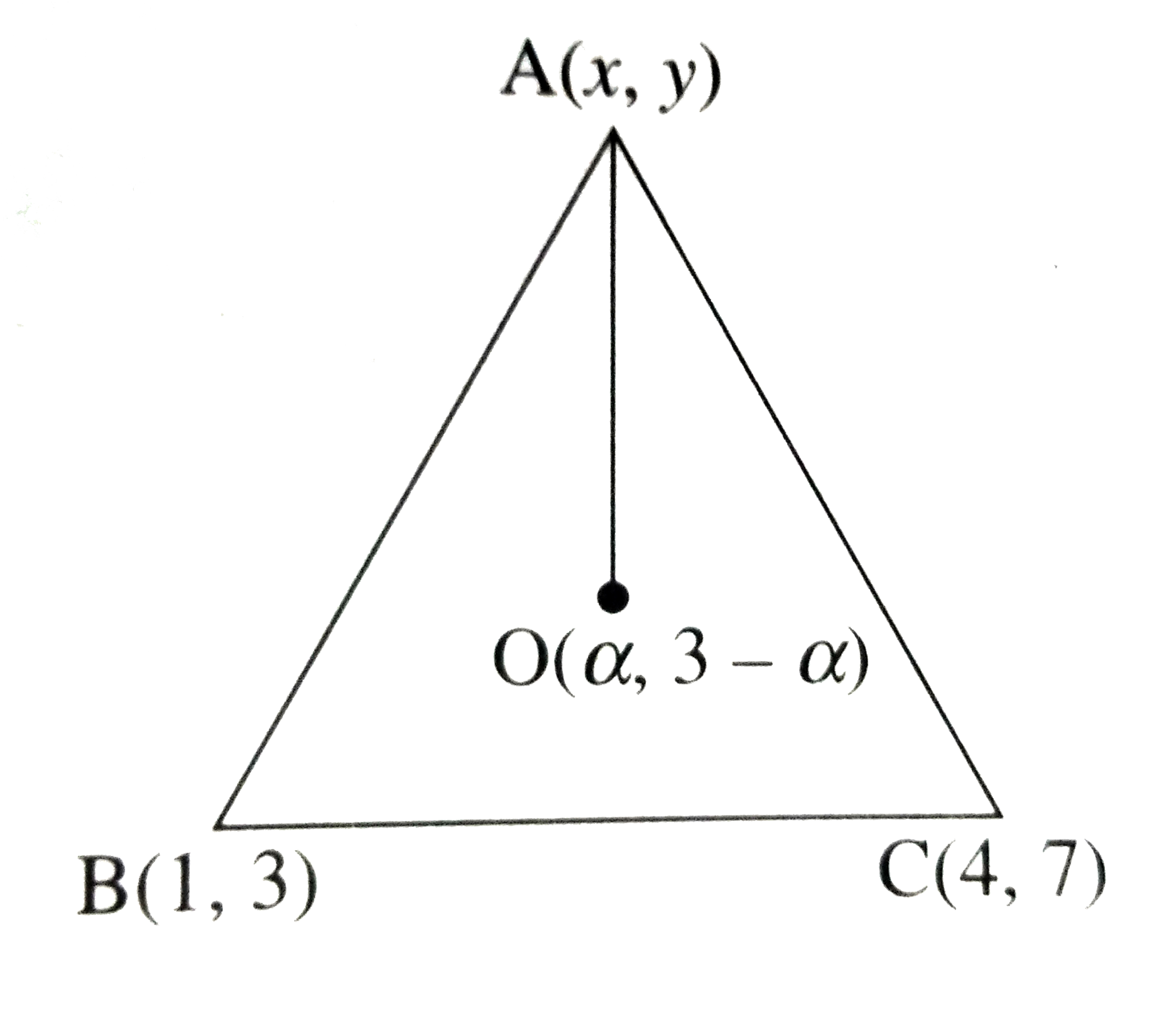
Orthocenter lies on the line x+y=2
Let orthocenter be O(α,3−α)
BO⊥AC
⇒y−7x−4α1−α=−1
⇒α−1α=y−7x−4
⇒1−1α=y−7x−4
⇒1α=1−y−7x−4
⇒α=x−4x−y+3
Also, AO⊥BC
⇒y−3+αx−α×43=−1
⇒4y=12+4α=−3x+3α
⇒α=−3x−4y+12
∴ The locus is x−4x−y+3=−3x−4y+12
Topper's Solved these Questions
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Comprehension Type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Comprehension Type
2 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
Similar Questions
Column I|Column II Two vertices of a triangle are (5,−1)and(−2,3) . If the orthocentre is the origin, then the coordinates of the third vertex are|p. (−4,−7) A point on the line x+y=4 which lies at a unit distance from the line 4x+3y=10 is|q. (−7,11) The orthocentre of the triangle formed by the lines x+y−1=0,x−y+3=0,2x+y=7 is|r. (2,−2) If 2a,b,c are in AP, then lines ax+by=c are concurrent at|s. (−1,2)
View SolutionTwo vertices of a triangle are A(2,1)andB(3,−2). The third vertex C lies on the line y=x+9. If the centroid of ΔABC lies on y-axis, find the coordinates of C and the centroid.
View SolutionIf two vertices of a triangle are (1,3) and (4,-1) and the area of triangle is 5 sq. units, then the angle at the third vertex lies in :
View SolutionIf two vertices of a triangle are (1,3) and (4,-1) and the area of triangle is 5 sq. units, then the angle at the third vertex lies in :
View SolutionTwo vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
View SolutionTwo vertices of a triangle are (4,−3)&(−2,5). If the orthocentre of the triangle is at (1,2), find coordinates of the third vertex .
View SolutionTwo vertices of a triangle are (3,−1)and(−2,3) and its orthocentre is at the origin,. Find the coordinates of its third vertex.
View SolutionIf two vertices of a triangle are (−2,3) and (5,−1) the orthocentre lies at the origin, and the centroid on the line x+y=7 , then the third vertex lies at
View SolutionIf two vertices of a triangle are (−2,3) and (5,−1) the orthocentre lies at the origin, and the centroid on the line x+y=7 , then the third vertex lies at (a)(7,4) (b) (8,14)(c) (12 ,21) (d) none of these
View SolutionTwo vertices of triangle are (2,-1) and (3,2) and third vertex lies on the line x+y=5. If the area of the triangle is 4 square units, then the third vertex is a. (0,50) or (4,1) b. (5,0) of (1,4) c. (5,0) or (4,1) d. (o,5) or (1,4)
View Solution
