A circle of radius 5 is tangent to the line $4 x - 3 y = 18$ at M(3, -2) and lies above the line. The equation of the circle is

A

$x^{2} + y^{2} - 6 x + 4 y - 12 = 0$

B

$x^{2} + y^{2} + 2 x - 2 y - 3 = 0$

C

$x^{2} + y^{2} + 2 x - 2 y - 23 = 0$

D

$x^{2} + y^{2} + 6 x + 4 y - 12 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

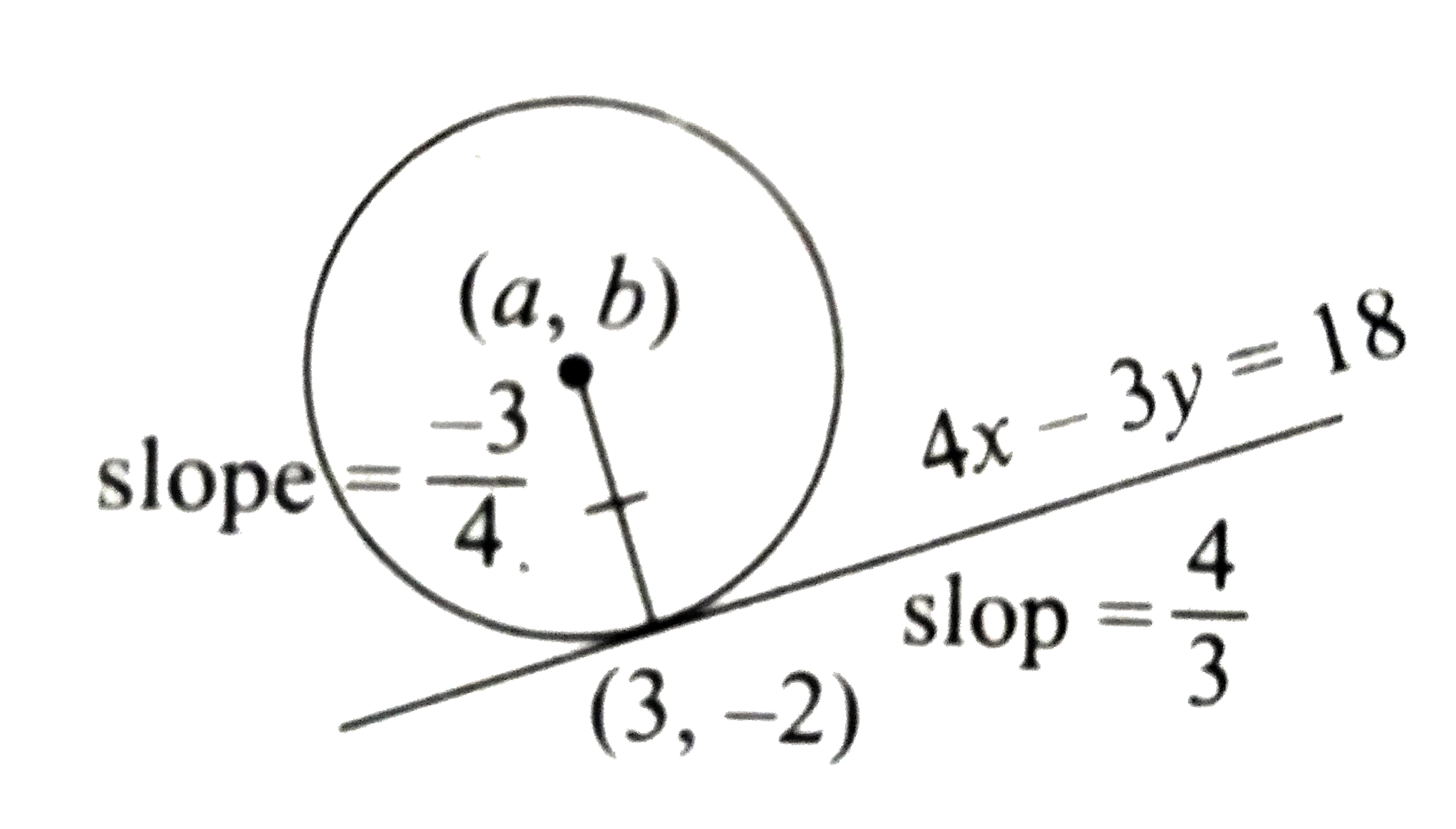
Let $\frac{x - 3}{cos θ} = \frac{y + 2}{sin θ} = 5$ , where $tan θ = \frac{- 3}{4}$
$\Rightarrow x = 5 cos θ + 3$
and $y = 5 sin θ - 2$
we have, $cos θ = \frac{- 4}{5}$ and $sin θ = \frac{3}{5}$
$∴ x = - 1$ and $y = 1$
$\Rightarrow$ centre $\equiv (- 1, 1)$
Hence, required equation of circle is
${(x + 1)}^{2} + {(y - 1)}^{2} - 25$
$\Rightarrow x^{2} + y^{2} + 2 x - 2 y - 23 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CIRCLES-Comprehension Type

Home
Ask Doubt
Profile