Question

A rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio $\lambda (\ne 1)$ is ellipse. Alos, find the eccentricity of the ellipse.

Explanation

From the figure,
In `DeltaPQB, cos theta =(PQ)/(PB)=(h)/(PA)`

Now, `(AP)/(PA)= (lambda)/(1)`
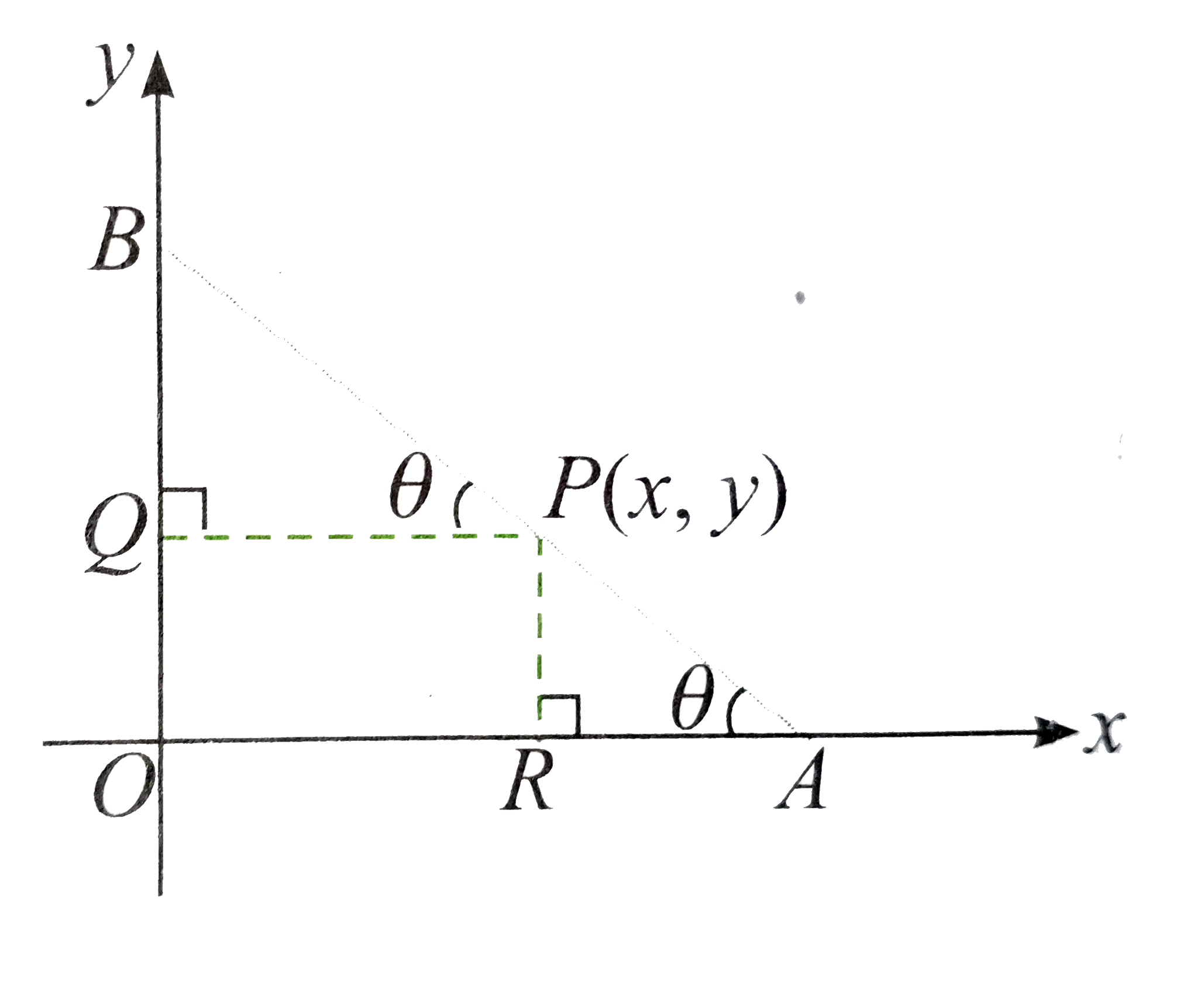
`rArr(AP)/(lambda)=(PB)/(1)=(AP+PB)/(lambda+1)=(AB)/(lambda+1)=(l)/(lambda+1)`
`:. AP=(lambdal)/(lambda+1) and PB=(l)/(lambda+1)`
`:. cos theta=(h(lambda+1))/(l)=and sin theta =(k(lambda+1))/(lambdal)`
Squaring and adding,
`(h^(2)(lambda+1)^(2))/(l^(2))+(k^(2)(lambda+1)
^(2))/(lamda^(2)l^(2))=1`
or `(x^(2))/(l^(2)/((lambda+1)^(2)))+(y^(2))/((lambda^(2)l^(2))/((lambda+1)^(2)))=1`
This is the equation of required locus, Clrarly this is the eqution of ellipse.
Let `lambdalt1`, then `e^(2) =1-(lambda^(2)l^(2))/((lambda+1)^(2)/(l^(2)/(lambda+1)^(2)))=1-lambda^(2)`
`:. e=sqrt(1-lambda^(2))`