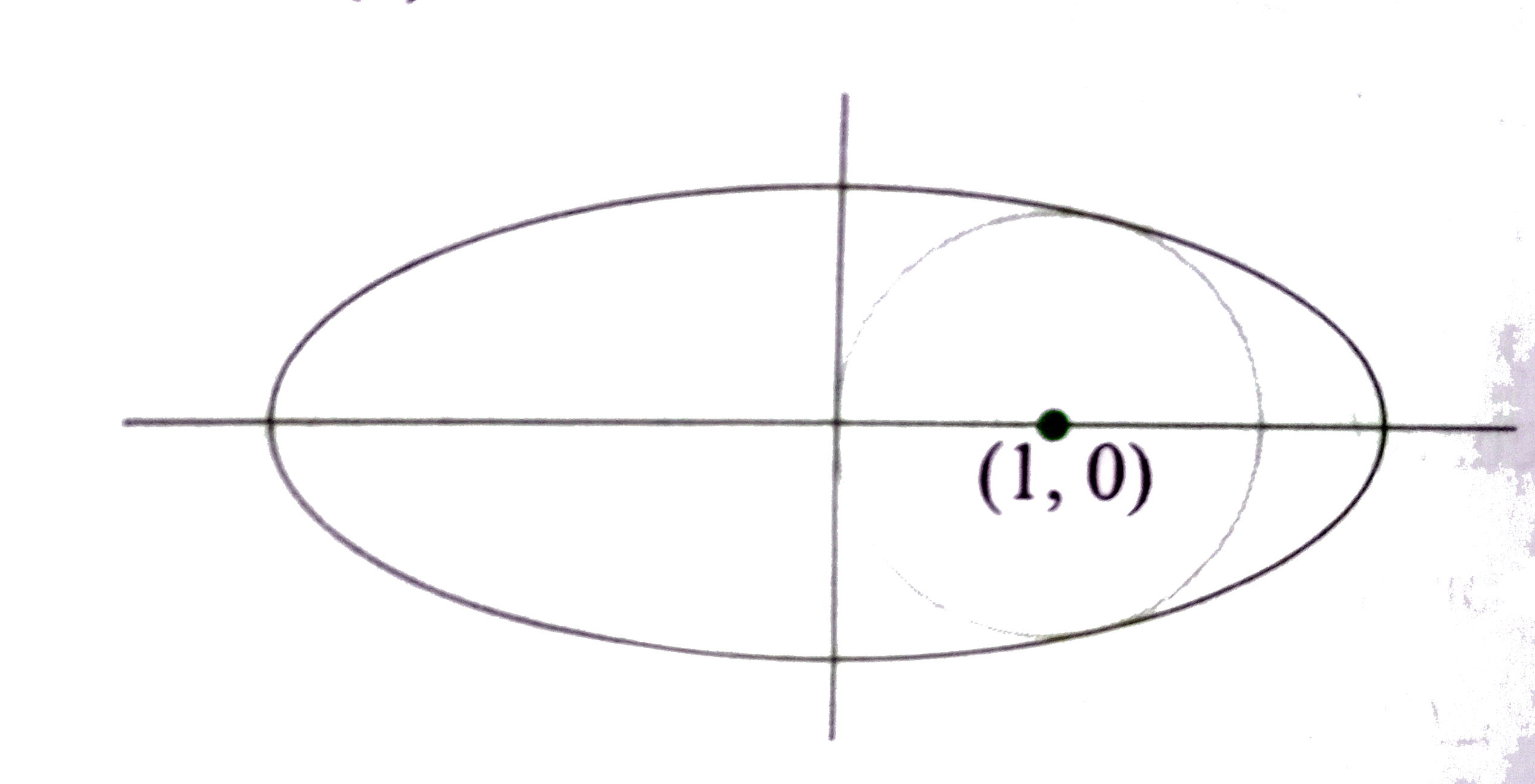
The ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The length of latus of ellipse is
2 units
√2units
3 units
2.5 units
Solving both equations we have
x2a2+1−(x−1)2b2=1
or b2x2+a2[1−(x−1)2]=a2b2
or (b2−a2)x2+2a2x−a2b2=0 (1)
For leat area, the circle.
Therefore, the discriminant of (1) is zero. Thus,
4a2+4a2b2(b2−a2)=0
or a2+b2(b2−a2)=0
or a2+b2(−a2e2)=0
or 1−be2e2=0
orb=1e
Also, a2=b21−e2=1e2(1−e2)
ora=1e√1−e2
Let S be the area of the ellipse. Then,
S=πab=πe2√1−e2=π√e4−e6
The area is minimum if (f)(e)=e2−e6 is maximum, i.e., when f'(e)=4e3−6e5=0
or √23 [ which is the point of maxima for f(e)]
So,S is the least when e=√2/3
Therfore, the ellipse is x2+y2=4.5
Length of loatus rectum of ellipe =2b2a=2×963√2=√2
Similar Questions
The ellipse x2a2+y2b2=1 is such that it has the least area but contains the circle (x−1)2+y2=1
The eccentricity of the ellipse isView SolutionThe area of the ellipse x2a2+y2b2=1 is
View SolutionIf the length of minor axis of the ellipse x2k2a2+y2b2=1 is equal to the length of transverse axis of hyperbola x2a2−y2b2=1,and the equation of ellipse is confocal with hyperbola then the value k is equal to
View SolutionIf eccentricity of the ellipse x2a2+1+y2a2+2=1 is 1√6, then the ratio of the length of the latus rectum to the length of the major axis is
View SolutionFor the ellipse x24+y23=1 , the ends of the two latus rectum are the four points
View SolutionLet the eccentricity of the hyperbola x2a2−y2b2=1 be the reciprocal to that of the ellipse x2+4y2=4. If the hyperbola passes through a focus of the ellipse, then the equation of the hyperbola, is
View Solutionif the line x- 2y = 12 is tangent to the ellipse x2b2+y2b2=1 at the point (3,−92) then the length of the latusrectum of the ellipse is
View SolutionArea of the ellipse x2a2+y2b2=1is πab
View SolutionAOB is the positive quadrant of the ellipse x2a2+y2b2=1 which has OA=a,OB=b . Then find the area between the arc AB and the chord AB of the ellipse.
View SolutionAOB is the positive quadrant of the ellipse x2a2+y2b2=1 in which OA=a,OB=b . Then find the area between the arc AB and the chord AB of the ellipse.
View Solution

