Solve for xandy:√3sinx+cosx=8y−y2−18,where0≤x≤4π,y∈R
To solve the equation √3sinx+cosx=8y−y2−18 where 0<x<4π and y∈R, we will follow these steps:
Step 1: Rearranging the Equation
We start with the equation:
√3sinx+cosx=8y−y2−18
Rearranging gives:
√3sinx+cosx+y2+8y+18=0
Step 2: Analyze the Right-Hand Side
The right-hand side can be expressed as a quadratic in y:
−y2−8y−18
To find the maximum value of this quadratic, we can complete the square:
−(y2+8y+18)=−((y+4)2−16)=−(y+4)2+16
Thus, the maximum value of −y2−8y−18 is 16 (when y=−4).
Step 3: Finding the Range of the Left-Hand Side
Now, we analyze the left-hand side √3sinx+cosx. This expression can be rewritten using the amplitude form:
√3sinx+cosx=2(√32sinx+12cosx)=2sin(x+π6)
The maximum value of 2sin(x+π6) is 2 and the minimum value is −2.
Step 4: Setting the Ranges Equal
From the previous steps, we have:
−2≤√3sinx+cosx≤2
And we found that:
−2≤−y2−8y−18≤16
For equality to hold, we need:
√3sinx+cosx=−2
Step 5: Solving for x
Setting √3sinx+cosx=−2:
2sin(x+π6)=−2
This simplifies to:
sin(x+π6)=−1
The general solution for sinθ=−1 is:
θ=3π2+2kπ(k∈Z)
Thus:
x+π6=3π2+2kπ
Solving for x:
x=3π2−π6+2kπ=9π6−π6+2kπ=8π6+2kπ=4π3+2kπ
Considering 0<x<4π:
- For k=0: x=4π3
- For k=1: x=4π3+2π=10π3
Both values 4π3 and 10π3 are within the range 0<x<4π.
Step 6: Solving for y
Now, substituting y back into the equation:
Setting −2=8y−y2−18:
y2+8y+16=0
Factoring gives:
(y+4)2=0
Thus, y=−4.
Final Solutions
The solutions are:
x=4π3,10π3,y=−4
We start with the equation:
√3sinx+cosx=8y−y2−18
Rearranging gives:
√3sinx+cosx+y2+8y+18=0
The right-hand side can be expressed as a quadratic in y:
−y2−8y−18
To find the maximum value of this quadratic, we can complete the square:
−(y2+8y+18)=−((y+4)2−16)=−(y+4)2+16
Thus, the maximum value of −y2−8y−18 is 16 (when y=−4).
Now, we analyze the left-hand side √3sinx+cosx. This expression can be rewritten using the amplitude form:
√3sinx+cosx=2(√32sinx+12cosx)=2sin(x+π6)
The maximum value of 2sin(x+π6) is 2 and the minimum value is −2.
From the previous steps, we have:
−2≤√3sinx+cosx≤2
And we found that:
−2≤−y2−8y−18≤16
For equality to hold, we need:
√3sinx+cosx=−2
Setting √3sinx+cosx=−2:
2sin(x+π6)=−2
This simplifies to:
sin(x+π6)=−1
The general solution for sinθ=−1 is:
θ=3π2+2kπ(k∈Z)
Thus:
x+π6=3π2+2kπ
Solving for x:
x=3π2−π6+2kπ=9π6−π6+2kπ=8π6+2kπ=4π3+2kπ
Considering 0<x<4π:
- For k=0: x=4π3
- For k=1: x=4π3+2π=10π3
Now, substituting y back into the equation:
Setting −2=8y−y2−18:
y2+8y+16=0
Factoring gives:
(y+4)2=0
Thus, y=−4.
The solutions are:
x=4π3,10π3,y=−4
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Concept Application Exercise 4.1
12 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Concept Application Exercise 4.2
6 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Solve for xandy:√3sinx+cosx=8y−y2−18,where0≤x≤4π,y∈R
View SolutionSolve for x and y 12sinx−2y2=21−8y−5cosx
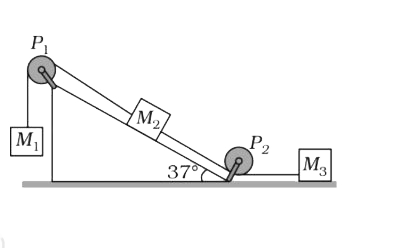
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionSolve the equation (sinx+cosx)1+sin2x=2, when 0≤x≤π
View Solutionydydxsinx=cosx(sinx−y22); where at x=π2,
View SolutionDiscuss the applicability of Rolles theorem on the function f(x)={x2+1, when 0≤x≤13−x, when 1<x≤2
View Solutiondydx for y=tan−1{√1+cosx1−cosx} ,where 0<x<π, is
View SolutionFind dydx for the function: y=(log)e√1+sinx1−sinx,wherex=π3
View SolutionWrite the range of the function f(x)=sin[x],where−π4≤x≤π4 .
View SolutionIf y=(sinx−cosx)sinx−cosx ,π4<x<3π4 find dy/dx
View Solution
