Match the equation in List I with the number of solutions in List II.

A
abcdqpsr
B
abcdqprs
C
abcdsrqp
D
abcdpqrs
Text Solution
The correct Answer is:A
a. cosax+cosbx=2,(a≠0,b≠0)
⇒ax=2nπandbx=2mπ,m,n∈Z
⇒ab=nm (here ab must be rational)
or LCM of a and b must exist. Also, x=0 is one solution So, equation has at least one solution.
b. cosx+cos(√2)x=2
⇒x=2nπand√2x=2mπ,m,n∈Z
⇒√2n=m, which is satisfied by m=n=0 only.
So, equation has only one solution x=0.
LCM of (1,√2) does not exist or 1√2 is irrational number.
c. cosax+cosbx=1,(a≠0,b≠0)
Clearly, equation has infinite solutions.
d. cosx+cosπx=−2
⇒cosx=−1andcosπx=−1
⇒x=(2k+1)πandπx=(2m+1)π,m,n∈Z
⇒(2k+1)π=(2m+1), which does not hold.
So, equation has no solution.
|
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Knowledge Check
Match the List-I and List-II:
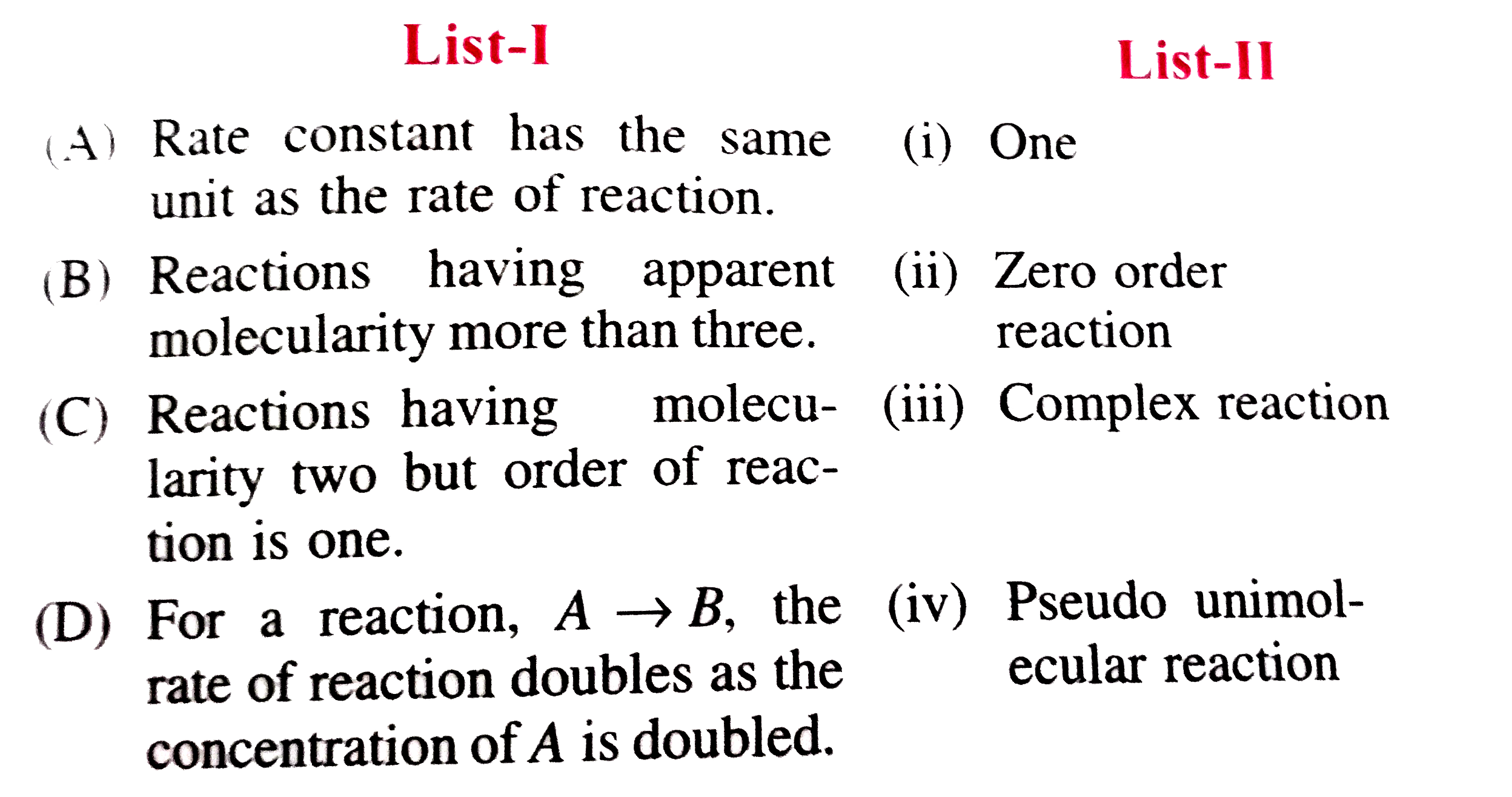 A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiii
A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiiiMatch the List-I and List-II:
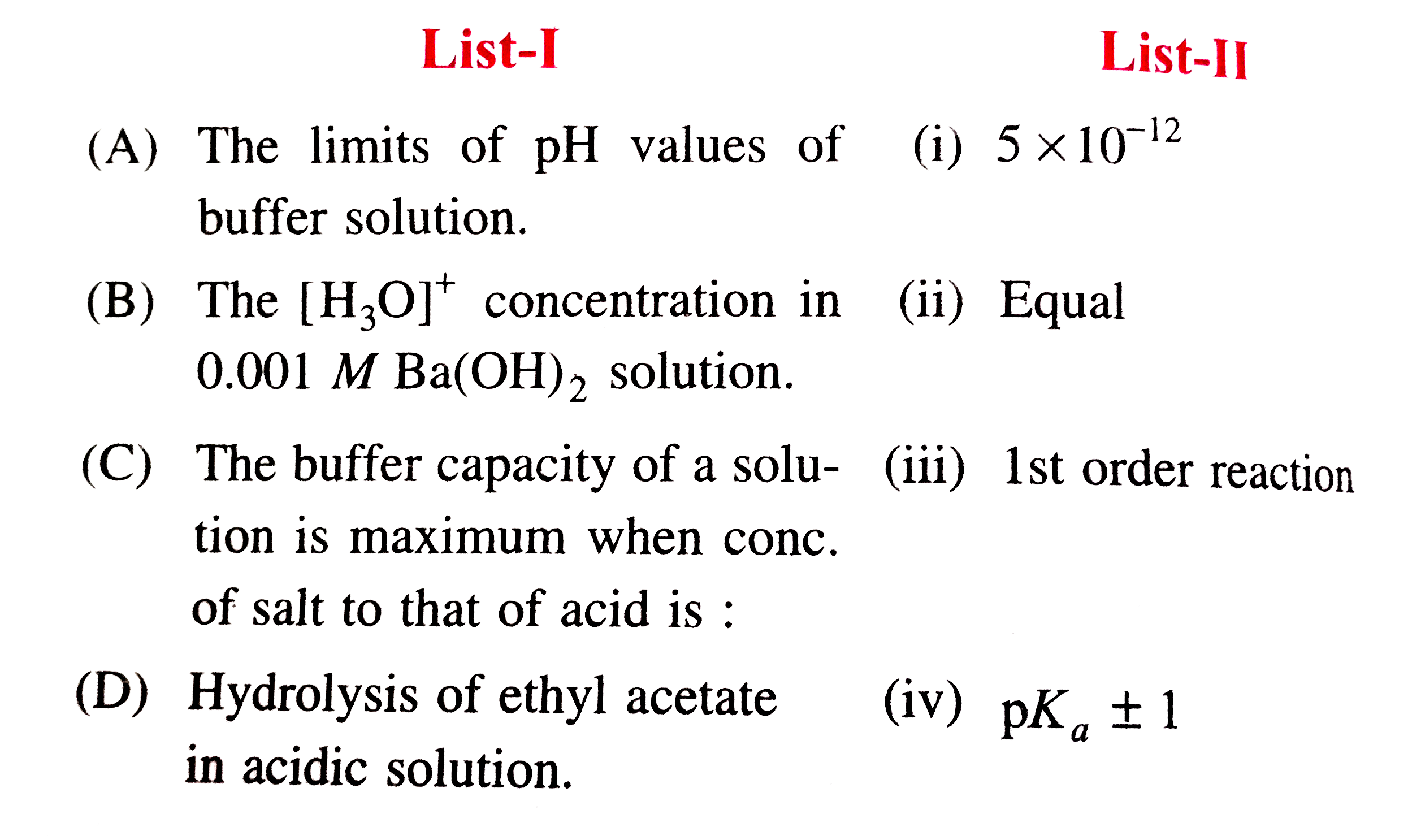 A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiii
A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiiiMatch the terms of List-I with those of List -II
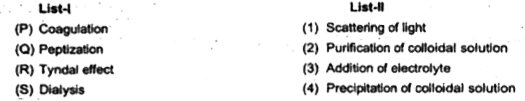 APQRS4312BPQRS2314CPQRS3142DPQRS2413
APQRS4312BPQRS2314CPQRS3142DPQRS2413
Match the statements given in the List-I with the equations given in List-II.
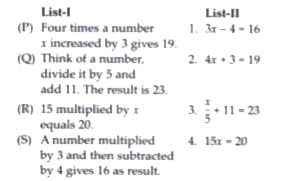
View SolutionMatch the List-I with List-II :

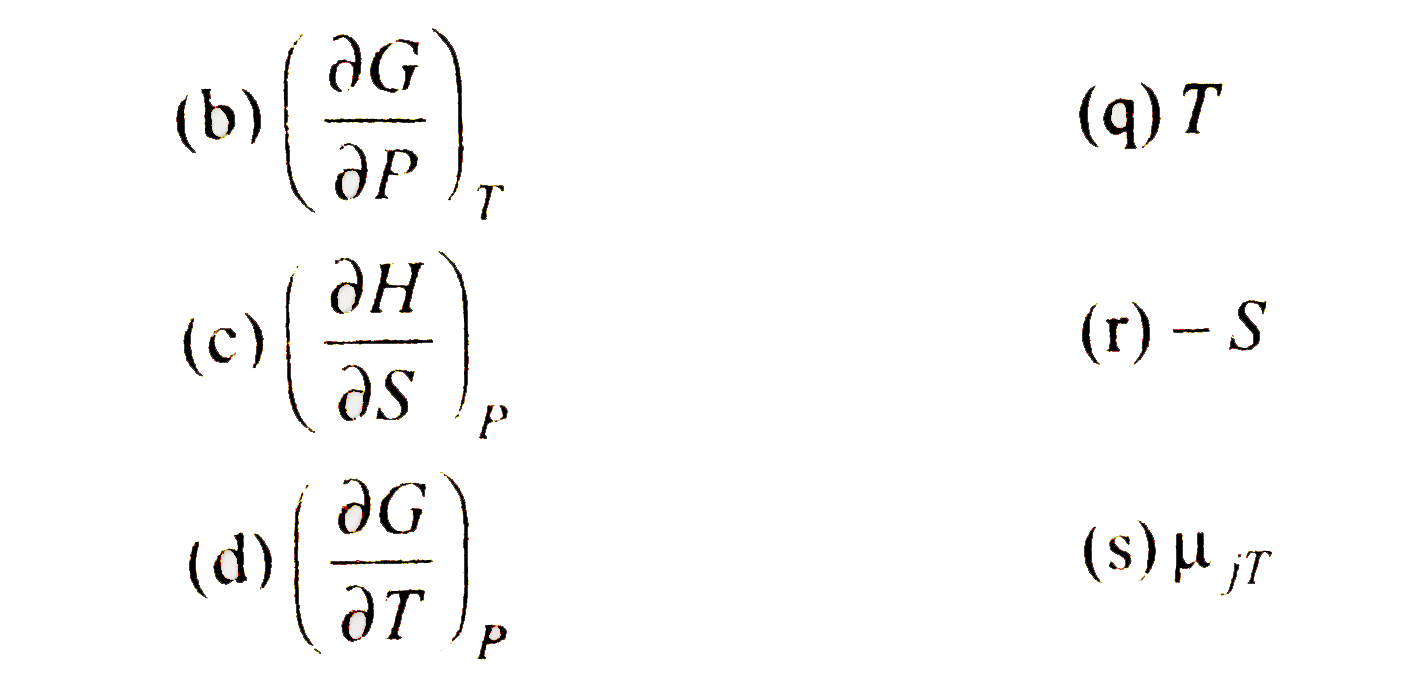
View SolutionMatch the list I with list II :
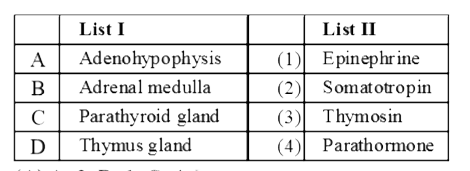
View SolutionMatch the List -I with List - II.
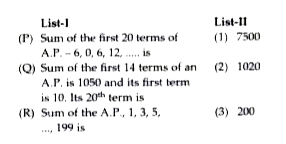
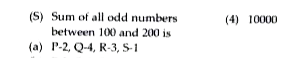
View SolutionMatch the ores of List-I with their composition in List-II

View Solution
