Two sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
0
1
2
infinite
The correct Answer is:C
To solve the problem step by step, we will follow the given information about the triangle and apply the Law of Cosines and area formulas.
Step 1: Identify the triangle and given values
We have a triangle with two sides:
- Side a=√6 (opposite the angle of 30 degrees)
- Side b=4
The angle opposite the smaller side a is given as 30∘.
Step 2: Use the Law of Cosines
According to the Law of Cosines:
c2=a2+b2−2abcos(C)
where C is the angle opposite side c.
Here, we need to find the length of side c (the third side). We can rearrange the formula to solve for c:
c2=(√6)2+42−2⋅√6⋅4⋅cos(30∘)
Substituting the values:
c2=6+16−2⋅√6⋅4⋅√32
c2=22−4√6√3
c2=22−4√18
c2=22−12=10
Thus, we have:
c=√10
Step 3: Determine the number of triangles
Since we have an angle of 30∘ opposite the side √6, we can check if there are two possible triangles. The angle opposite the longer side (4) can be calculated using the Law of Sines:
asin(A)=bsin(B)=csin(C)
Given that A=30∘, we can find B and check if it leads to a valid triangle.
Step 4: Calculate the area of the triangle
The area A of a triangle can be calculated using the formula:
Area=12⋅a⋅b⋅sin(C)
Substituting the known values:
Area=12⋅√6⋅4⋅sin(30∘)
Since sin(30∘)=12:
Area=12⋅√6⋅4⋅12=√6
Summary of Results
- The length of the third side c is √10.
- Two triangles are possible due to the ambiguous case of the triangle.
- The area of each triangle is √6.
We have a triangle with two sides:
- Side a=√6 (opposite the angle of 30 degrees)
- Side b=4
According to the Law of Cosines:
c2=a2+b2−2abcos(C)
where C is the angle opposite side c.
c2=(√6)2+42−2⋅√6⋅4⋅cos(30∘)
Substituting the values:
c2=6+16−2⋅√6⋅4⋅√32
c2=22−4√6√3
c2=22−4√18
c2=22−12=10
Thus, we have:
c=√10
Since we have an angle of 30∘ opposite the side √6, we can check if there are two possible triangles. The angle opposite the longer side (4) can be calculated using the Law of Sines:
asin(A)=bsin(B)=csin(C)
Given that A=30∘, we can find B and check if it leads to a valid triangle.
The area A of a triangle can be calculated using the formula:
Area=12⋅a⋅b⋅sin(C)
Substituting the known values:
Area=12⋅√6⋅4⋅sin(30∘)
Since sin(30∘)=12:
Area=12⋅√6⋅4⋅12=√6
- The length of the third side c is √10.
- Two triangles are possible due to the ambiguous case of the triangle.
- The area of each triangle is √6.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Multiple Correct Answers Type13videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives1videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives10videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
A triangle is not possible with sides of length (in cm)
A6,4,10B5,3,7C7,8,9D3.6,5.4,8 - Question 2 - Select One
The lengths of two sides of a triangle are 50 inches and 63 inches. The angle opposite the 63-inch side is 66∘ . How many degrees are in largest angle of the triangle ?
A66∘B67∘C68∘D71∘
Two sides of a triangle are 2√2and2√3cm and the angle opposite to the shorter side of the two is π4. The largest possible length of the third side is
View SolutionStatement-1: If the lengths of two sides of a triangle are roots of the equation x2−12x+35=0 and the angle opposite to third side is obtuse, then the square of the length of the third side is greater than 74.
Statement- 2: In a !ABC,cosC=a2+b2−c22abView SolutionTwo sides of a triangle have lengths of 5 and 19. Can the third side have a length of 13?
View SolutionTwo sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionFind the length of side BC in the given triangle.
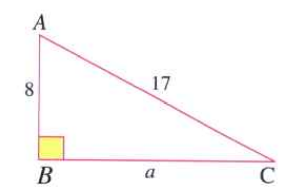 View Solution
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View Solution