Let ABC and AB'C be two non-congruent triangles with sides BC=B'C=5, AC=6, and ∠A is fixed. If A1 and A2 are the area of the two triangles ABC and AB'C, then the value of A21+A22−2A1A2cos2A(A1+A2)2 is
9/36
25/36
25/16
16/25
The correct Answer is:B
To solve the problem, we need to find the value of the expression
A21+A22−2A1A2cos2A(A1+A2)2
where A1 and A2 are the areas of triangles ABC and AB′C respectively, with given conditions.
Step 1: Determine the areas A1 and A2
The area of a triangle can be calculated using the formula:
A=12×base×height
For triangles ABC and AB′C, we can express the areas in terms of the sides and the sine of angle A:
A1=12×BC×h1=12×5×h1
A2=12×B′C×h2=12×5×h2
where h1 and h2 are the heights from point A to line BC and B′C respectively.
Step 2: Express heights in terms of angle A
Using the sine function, we can express the heights h1 and h2:
h1=AC⋅sinA=6⋅sinA
h2=AC⋅sinA=6⋅sinA
Thus, we have:
A1=12×5×(6sinA)=15sinA
A2=12×5×(6sinA)=15sinA
Step 3: Calculate A21 and A22
Since both areas are equal, we have:
A1=A2=15sinA
Thus,
A21=(15sinA)2=225sin2A
A22=(15sinA)2=225sin2A
Step 4: Substitute into the expression
Now we substitute A1 and A2 into the expression:
A21+A22=225sin2A+225sin2A=450sin2A
Next, we calculate 2A1A2cos2A:
2A1A2=2×(15sinA)×(15sinA)=450sin2A
Thus,
2A1A2cos2A=450sin2Acos2A
Step 5: Calculate the denominator
Now, we calculate (A1+A2)2:
A1+A2=15sinA+15sinA=30sinA
(A1+A2)2=(30sinA)2=900sin2A
Step 6: Substitute everything into the expression
Now we substitute everything into the original expression:
450sin2A−450sin2Acos2A900sin2A
Step 7: Simplify the expression
Factor out 450sin2A:
=450sin2A(1−cos2A)900sin2A
This simplifies to:
=450(1−cos2A)900=1−cos2A2
Using the identity 1−cos2A=2sin2A, we get:
=2sin2A2=sin2A
Final Result
Thus, the value of the expression is:
sin2A
A2=12×B′C×h2=12×5×h2
h2=AC⋅sinA=6⋅sinA
A2=12×5×(6sinA)=15sinA
A22=(15sinA)2=225sin2A
(A1+A2)2=(30sinA)2=900sin2A
Topper's Solved these Questions
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Multiple Correct Answers Type
13 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives
1 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
Similar Questions
A1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View SolutionIf a1anda2 are two non- collinear unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
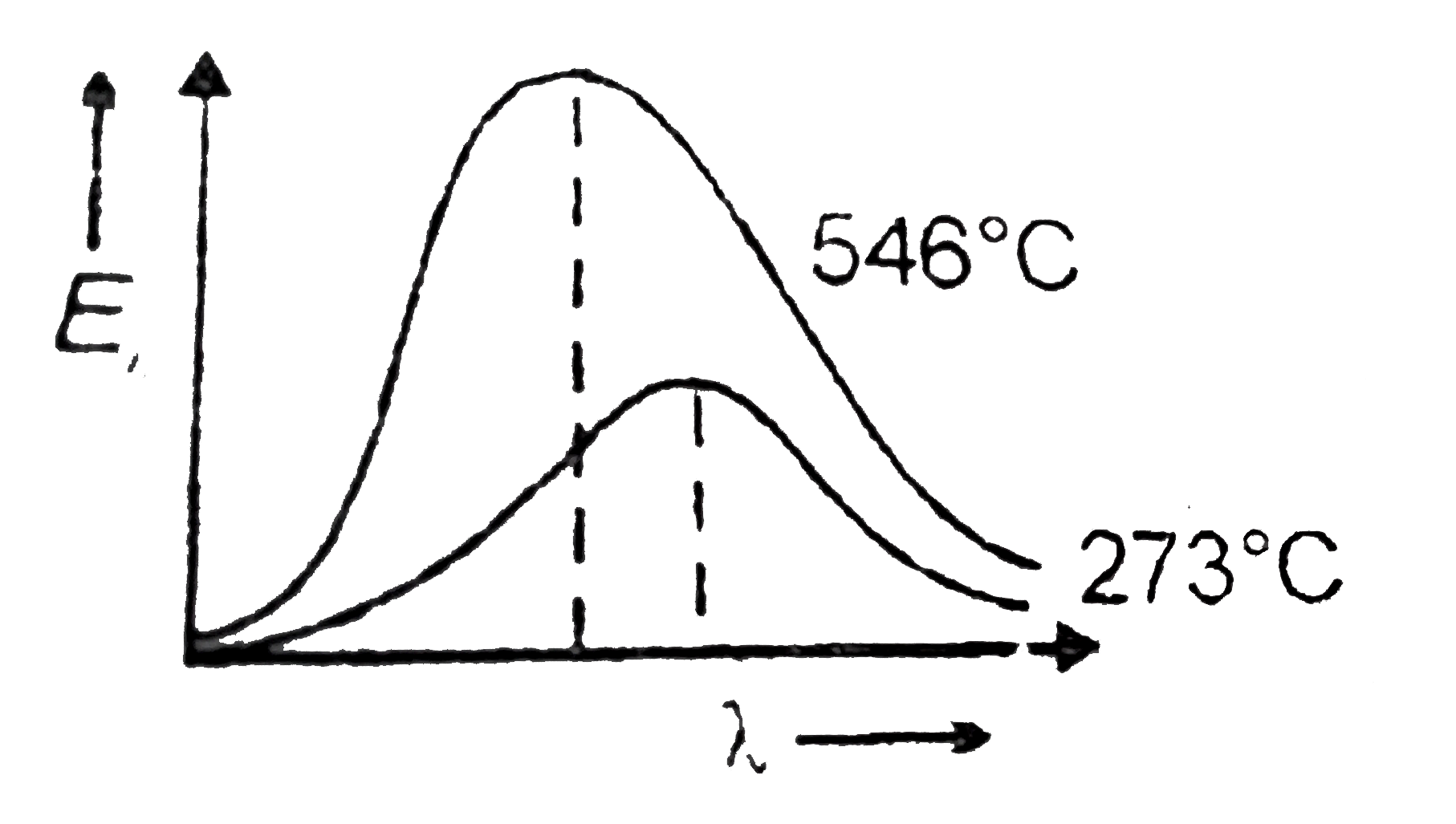
View SolutionThe spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
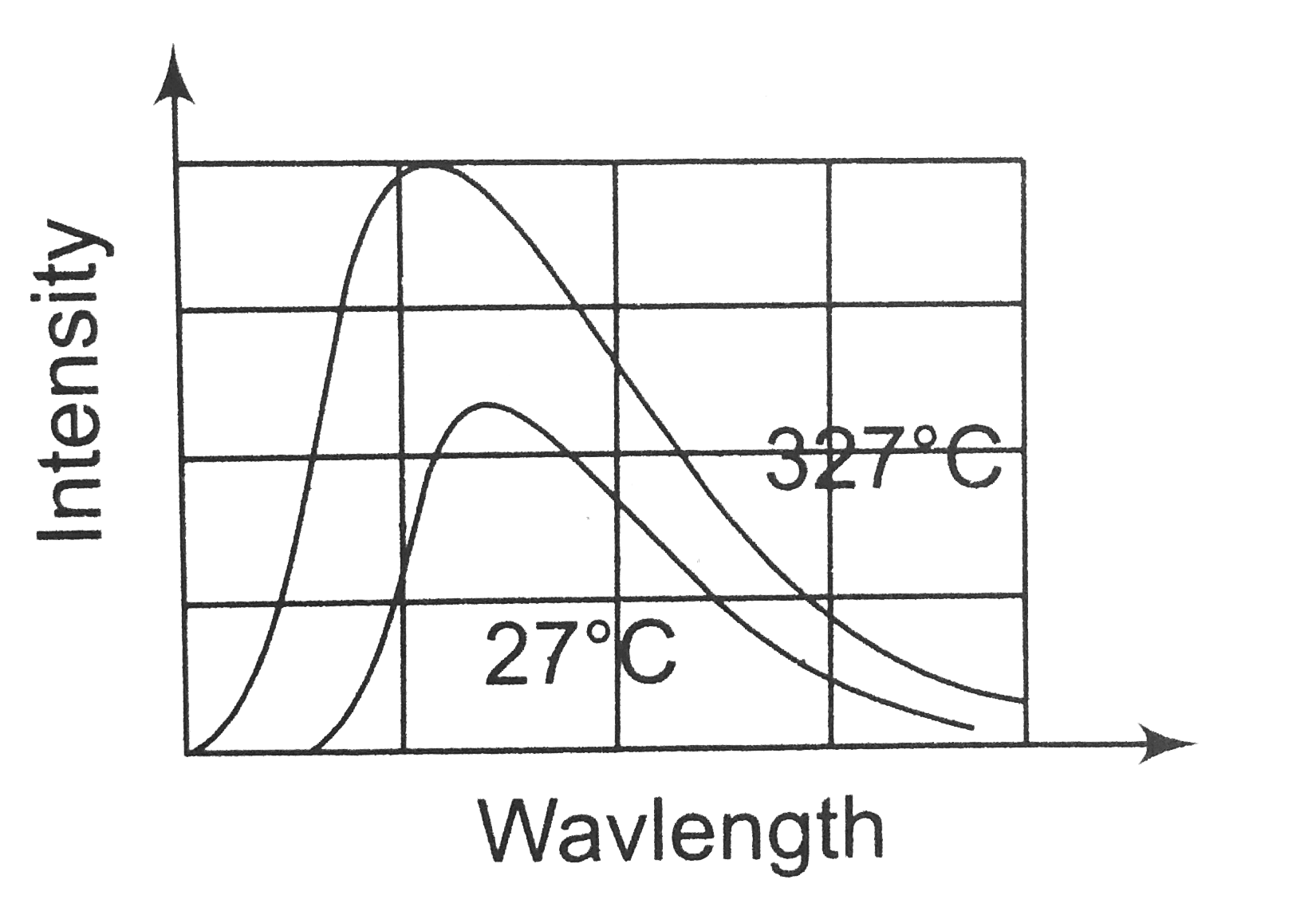
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View SolutionLet A1A2A3……………….A14 be a regular polygon with 14 sides inscribed in a circle of radius 7 cm. Then the value of (A1A3)2+(A1A7)2+(A3A7)2 (in square cm) is……………..
View SolutionIf a1,a2,a3,a4,a5 are consecutive terms of an arithmetic progression with common difference 3, then the value of ∣∣ ∣ ∣∣a23a2a1a24a3a2a25a4a3∣∣ ∣ ∣∣ is
View SolutionIf a1>0 for all i=1,2,…..,n. Then, the least value of
(a1+a2+……+an)(1a1+1a2+…+1an), is
View SolutionIf a1,a2,a3,a4 and a5 are in AP with common difference ≠0, find the value of 5∑i=1ai when a3=2.
View SolutionIf →a1and→a2 are two non-collinear unit vectors and if ∣∣→a1+→a2∣∣=√3, then the value of (→a1−→a2).(2→a1+→a2) is :
View Solution
