ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.Ar(△ABD)=k2,ar(△BCD)=k3 then ar(△ACD) is
√k21+k22+k23
√k1k2k3k1+k2+k3
√∣∣k21+k22−k23∣∣
√∣∣k22−k21−k23∣∣
The correct Answer is:C
To find the area of triangle ACD in the tetrahedron ABCD, given that triangles ABC, ABD, and ACD have right angles at A, we can use the relationship between the areas of these triangles.
1. Identify the Areas of Triangles:
- Let the area of triangle ABC be ar(ABC)=k1.
- Let the area of triangle ABD be ar(ABD)=k2.
- Let the area of triangle BCD be ar(BCD)=k3.
- We need to find the area of triangle ACD, denoted as ar(ACD)=k4.
2. Use the Relationship of Areas:
- In a tetrahedron, if three faces are right triangles at a common vertex, the areas of these triangles satisfy the following relationship:
ar(ABC)2+ar(ABD)2+ar(ACD)2=ar(BCD)2
- Substituting the known areas into this equation gives:
k21+k22+k24=k23
3. Rearranging the Equation:
- To isolate k24, we rearrange the equation:
k24=k23−k21−k22
4. Taking the Square Root:
- To find k4, we take the square root of both sides:
k4=√k23−k21−k22
5. Conclusion:
- Therefore, the area of triangle ACD is:
ar(ACD)=√k23−k21−k22
Final Answer:
The area of triangle ACD is √k23−k21−k22.
- Let the area of triangle ABC be ar(ABC)=k1.
- Let the area of triangle ABD be ar(ABD)=k2.
- Let the area of triangle BCD be ar(BCD)=k3.
- We need to find the area of triangle ACD, denoted as ar(ACD)=k4.
- In a tetrahedron, if three faces are right triangles at a common vertex, the areas of these triangles satisfy the following relationship:
ar(ABC)2+ar(ABD)2+ar(ACD)2=ar(BCD)2
- Substituting the known areas into this equation gives:
k21+k22+k24=k23
- To isolate k24, we rearrange the equation:
k24=k23−k21−k22
- To find k4, we take the square root of both sides:
k4=√k23−k21−k22
- Therefore, the area of triangle ACD is:
ar(ACD)=√k23−k21−k22
The area of triangle ACD is √k23−k21−k22.
Topper's Solved these Questions
Similar Questions
In △ABC, if Rr≤2, and a=2, then △ is equal to (△=ar(△ABC)).
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn △ABC, if ar (△ABC)=8. Then, a2sin(2B)+b2sin(2A) is equal to
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn △ABC, if √3sinC=2secA−tanA, then prove that triangle is right angled.
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
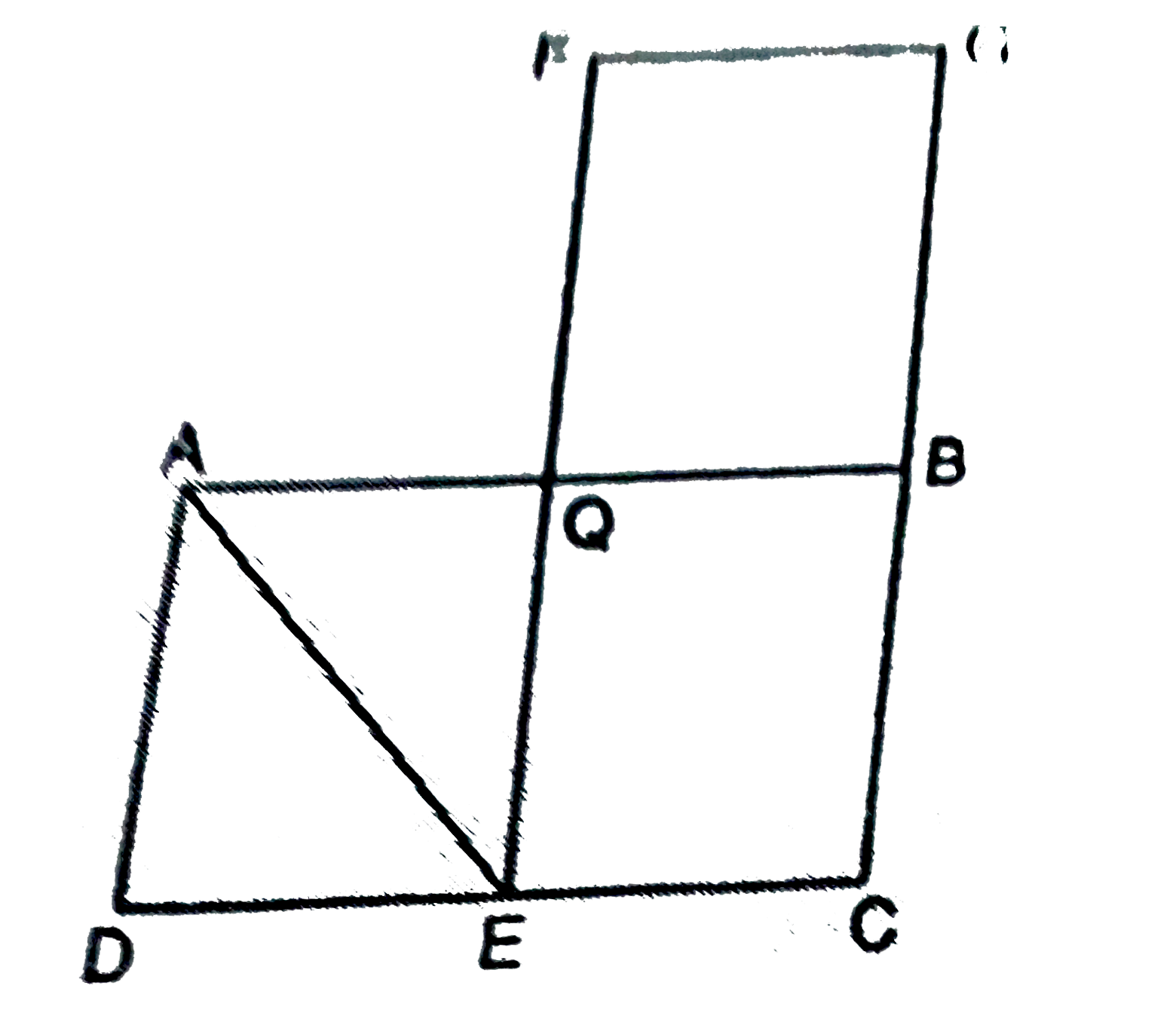
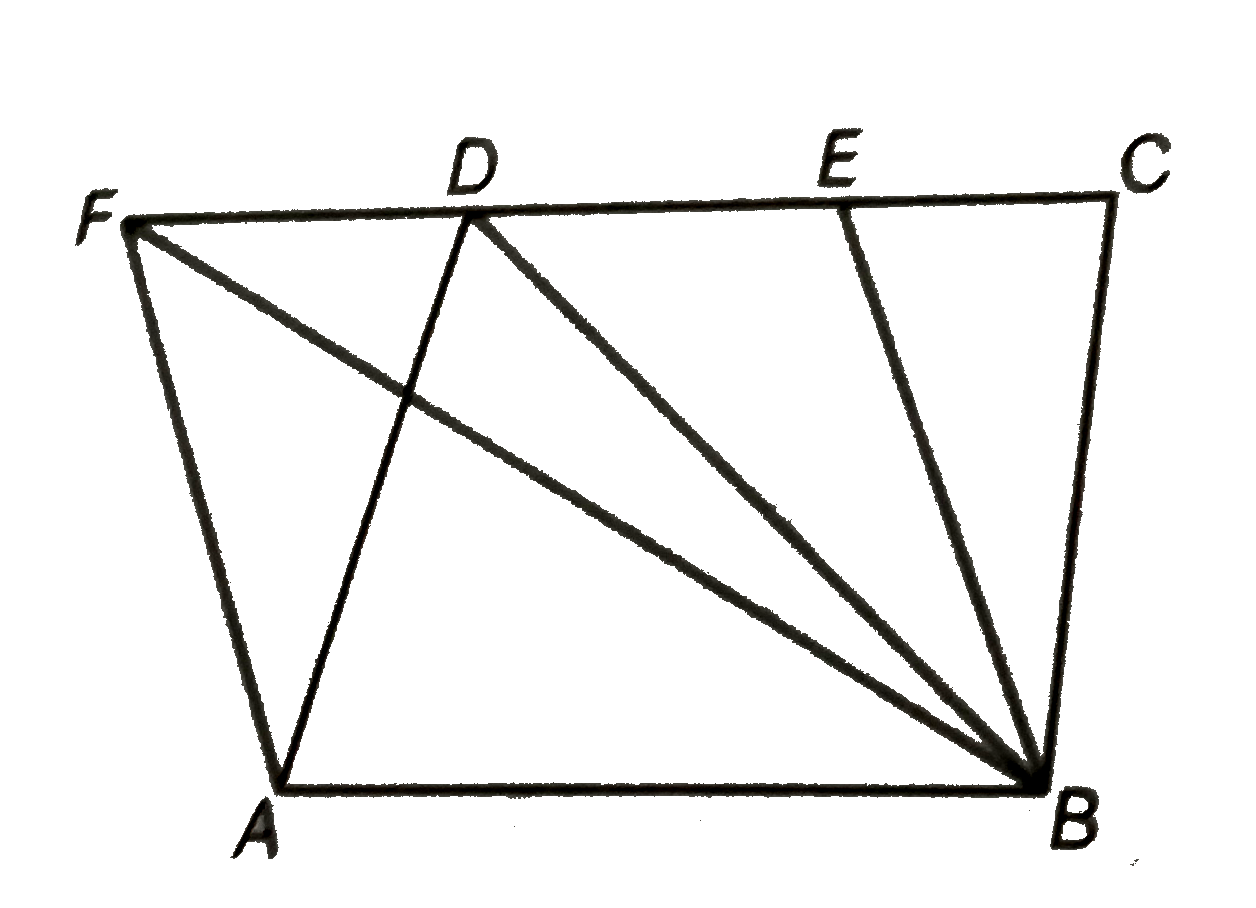
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
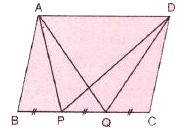
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View Solution
