Question

Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If $a,b,c\text{and}d$ denote the lengths of sides of the quadrilateral, prove that $2\le a_2+b_2+c_2+d_2\le 4$

Explanation

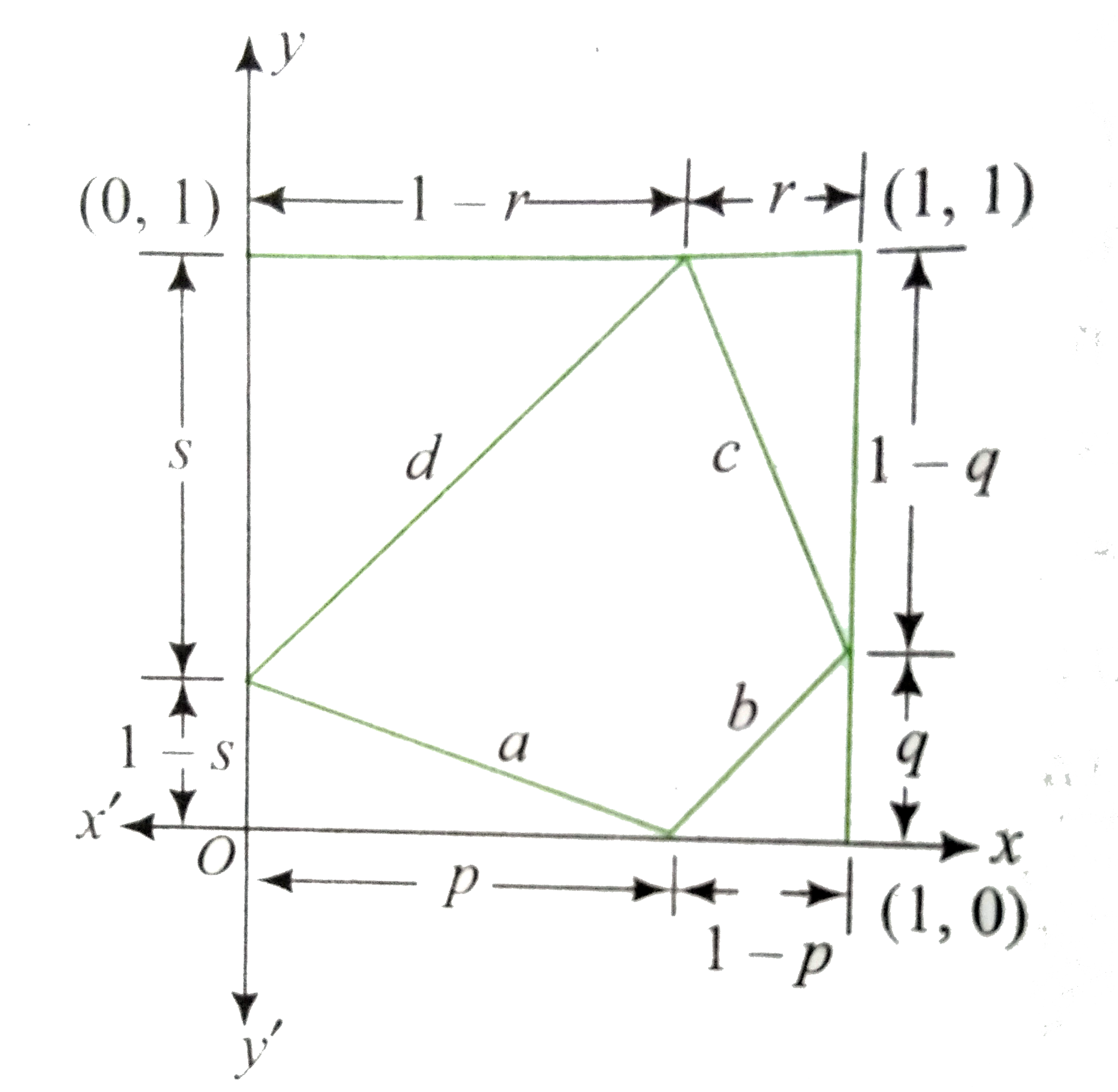
From the figure
`a^(2) = p^(2) + (1 - s)^(2)`
b^(2) = (1 - p)^(2) + q^(2)`
`a^(2) + b^(2) + c^(2) + d^(2)= [ p^(2) + (1 - p)^(2)] + [q^(2) + ( 1 - q)^(2) ] `
` [ r^(2) + (1 - r)^(2)] + [s^(2) + ( 1 - s)^(2) ]` , where p , q , r, s `in`[0, 1]
Now consider the function
`y = x^(2) + (1 - x)^(2), 0 le x le 1`
`rArr y = 2x^(2) - 2x + 1 = 2 (x - (1)/(2))^(2) + (1)/(2)`
Hence, minimum value is `1//2` when x = `1//2` and maximum value is at x = 1 , which is 1. Therefore, minimum value of `a^(2) + b^(2) + c^(2) d^(2)` is `1//2+ 1//2 + 1//2 +1//2 = 2` and maximum value is `1 + 1 + 1 + 1 = 4`.