The range of a for which the equation x2+x−4=0 has its smaller root in the interval (−1,2)is (−∞,−3) b. (0,3) c. (0,∞) d. (−∞,−3)∪(0,∞)
(−∞,−3)
(0, 3)
(0,∞)
(−∞,−3)∪(0,∞)
The correct Answer is:A
Clearly , f(−1)>0,f(2)<0
Now ,
f(0)=−4<0
⇒f(−1)=1−a−4>0
and f(2)=4+2a−4<0
⇒a<−3anda<0
⇒a∈(−∞),−3)
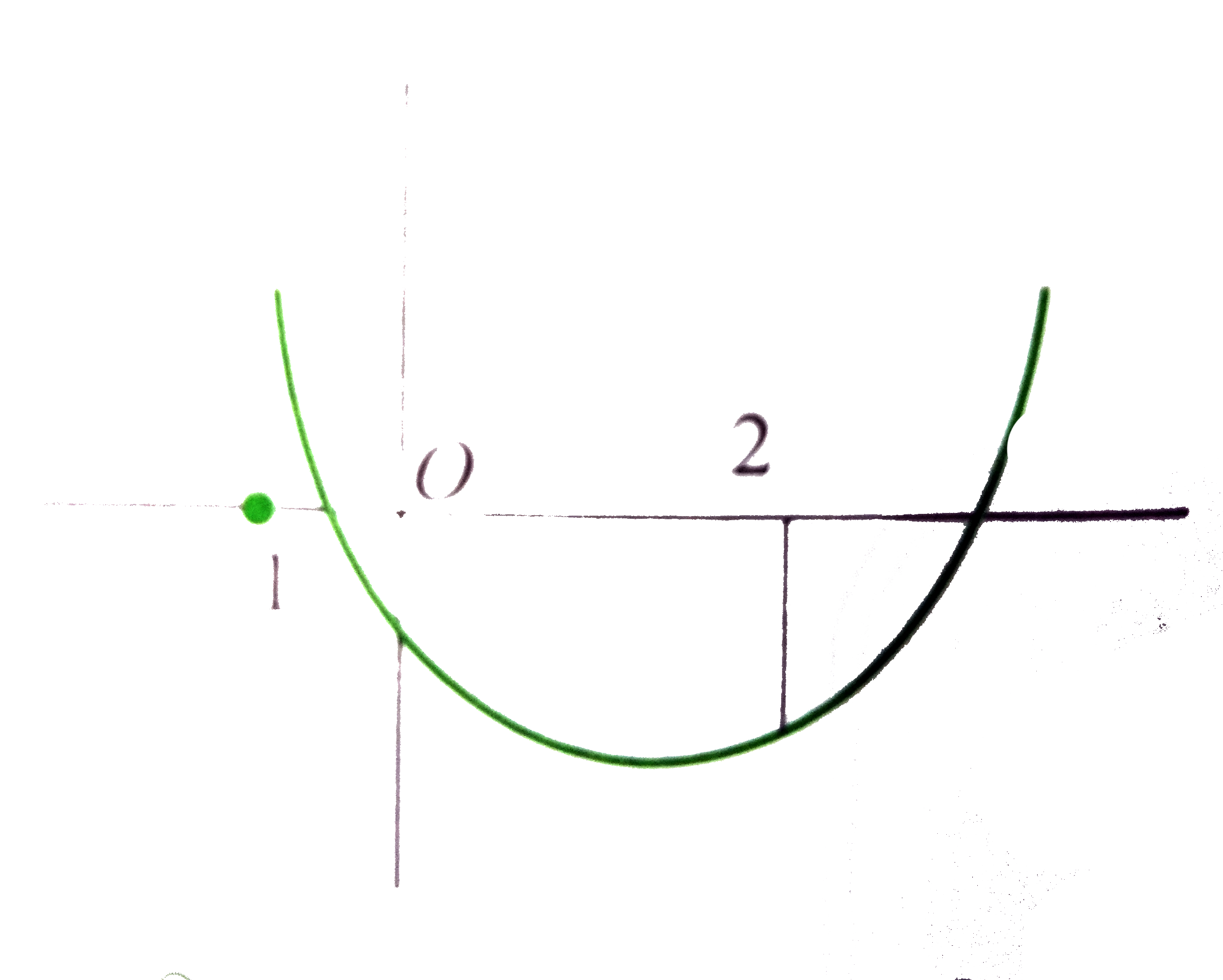
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.13
9 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
The range of a for which the equation x2+ax−4=0 has its smaller root in the interval (−1,2)is a. (−∞,−3) b. (0,3) c. (0,∞) d. (−∞,−3)∪(0,∞)
View SolutionTh range of k for which the inequaliity kcos2x−kcosx+1≥0∀x∈(−∞,∞)is
View SolutionTh range of k for which the inequaliity kcos2x−kcosx+1≥0∀x∈(−∞,∞)is
View SolutionThe set of all values of 'a' for which the quadratic equation 3x2+2(a2−3a+2)=0 possess roots of opposite sign, is
a.(−∞,1) b. (−∞,0) c. (1,2) d. (3/2,2)
View SolutionThe function f(x)=cot−1x+x increases in the interval (a) (1, ∞) (b) (−1, ∞) (c) (−∞, ∞) (d) (0, ∞)
View SolutionIf the difference between the roots of the equation x2+ax+1=0 is less than √5 , then the set of possible values of a is (1) (−3,3) (2) (−3,∞) (3) (3,∞) (4) (−∞,−3)
View SolutionFind the set of values of a for which the equation |x−1|2+(a−1)|x−1|+1=0 has a solution, [2,5] b. [−3,−1] c. [0,∞) d. (−∞,−1]
View SolutionThe values of a for which the integral ∫20|x−a|dx≥1 is satisfied are (a)(2,∞) (b) (−∞,0) (c)(0,2) (d) none of these
View SolutionFor x2−(a+3)|x|+4=0 to have real solutions, the range of a is a. (−∞,−7]∪[1,∞) b. (−3,∞) c. (−∞,−7) d. [1,∞)
View SolutionThe complete set of values of a so that equation sin4x+asin2x+4=0 has at least one real root is (A) (−∞,−5] (B) (−∞,4]∪[4,∞) (C) (−∞,−4] (D) [4,∞)
View Solution
