Consider the quadration which has two distinct real roots belonging to the interval (1,2).
The least value of b is
4
6
7
5
The correct Answer is:2
Let be
the correspoding quadratic expression and be the roots of .
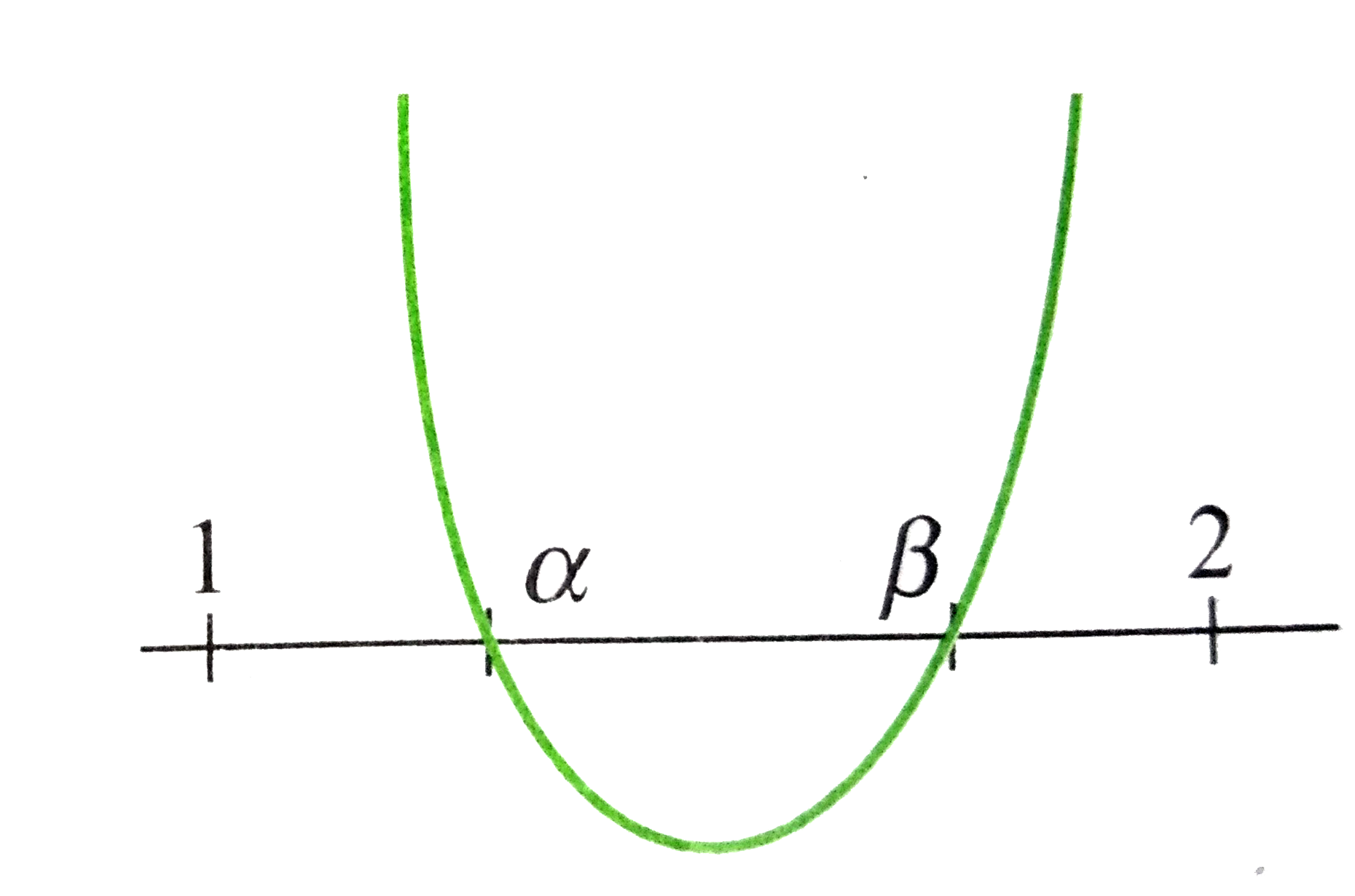
Then,
Now,
As and both are integers and , and , so
Now,
Similarly,
As , so
Also,
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
If ax2+bx+c=0 have two distinct roots lying int eh interval (0,1),a,b,c εN The least value of b is
View SolutionIf the quadratic equation a1x2−a−(2)x+a3=0 where a1,a2,a3∈N has two distinct real roots belonging to the interval (1,2) then least value of a1 is_______
View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1),a,b,cEψlonN The least value of log5abc is
View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1);a,b,∈N, then the least value of a , is
View SolutionIf the equation ax2+bx+c=0,a,b,c,∈ R have non -real
roots, then
View SolutionIf α and β are the roots of the equation ax2+bx+c=0 then ax2+bx+c=a(x−α)(x−β).Also if a quadratic equation f(x)=0 has both roots between mandn then f(m)andf(n) must have same sign. It is given that all the quadratic equations are of form ax2−bx+c=0 a,b,cεN have two distict real roots between 0and1. The least value of c for which such a quadratic equation exists is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionIf α and β are the roots of the equation ax2+bx+c=0 then ax2+bx+c=a(x−α)(x−β).Also if a quadratic equation f(x)=0 has both roots between mandn then f(m)andf(n) must have same sign. It is given that all the quadratic equations are of form ax2−bx+c=0 a,b,cεN have two distict real roots between 0and1.The least value of b for which such a quadratic equation exists is (A) 3 (B) 4 (C) 5 (D) 6
View SolutionIf α and β are the roots of the equation ax2+bx+c=0 then ax2+bx+c=a(x−α)(x−β).Also if a quadratic equation f(x)=0 has both roots between mandn then f(m)andf(n) must have same sign. It is given that all the quadratic equations are of form ax2−bx+c=0 a,b,cεN have two distict real roots between 0and1.The least value of a for which such a quadratic equation exists is (A) 3 (B) 4 (C) 5 (D) 6
View SolutionIf ax2+bx+6=0 does not have two distinct real roots, a∈R and b∈R, then the least value of 3a+b is
View SolutionIf ax2+bx+10=0 does not have two distinct real roots, then the least value of 5a + b, is
View Solution
