ifωandω2 are the nonreal cube roots of unity and [1/(a+ω)]+[1/(b+ω)]+[1/(c+ω)]=2ω2 and [1/(a+ω)2]+[1/(b+ω)2]+[1/(c+ω)2]=2ω , then find the value of [1/(a+1)]+[1/(b+1)]+[1/(c+1)].
To solve the problem, we need to analyze the given equations and use the properties of cube roots of unity. Let's break it down step by step.
Step 1: Understanding the Cube Roots of Unity
The non-real cube roots of unity are given by:
- ω=e2πi/3=−12+i√32
- ω2=e−2πi/3=−12−i√32
These satisfy the equation:
1+ω+ω2=0
Step 2: Rewrite the Given Equations
We are given two equations:
1. 1a+ω+1b+ω+1c+ω=2ω2
2. 1(a+ω)2+1(b+ω)2+1(c+ω)2=2ω
Step 3: Generalize the Form
We can generalize the form:
1a+x+1b+x+1c+x=2x
for x=ω and x=ω2.
Step 4: Find the Polynomial
From the generalized form, we can derive:
3x2+2(a+b+c)x+(ab+ac+bc)(a+x)(b+x)(c+x)=2x
Cross-multiplying gives us:
3x3+2(a+b+c)x2+(ab+ac+bc)x−2abc=0
Step 5: Roots of the Polynomial
Since ω and ω2 are roots, let the third root be α. By Vieta's formulas:
α+ω+ω2=0⟹α=−(ω+ω2)=1
Step 6: Substitute α into the Equation
Now we substitute α=1 back into the polynomial:
1a+1+1b+1+1c+1
Step 7: Find the Value
We need to evaluate:
1a+1+1b+1+1c+1
Using the same form we derived:
1a+x+1b+x+1c+x=2x
for x=1:
1a+1+1b+1+1c+1=2
Final Answer
Thus, the value of 1a+1+1b+1+1c+1 is:
2
The non-real cube roots of unity are given by:
- ω=e2πi/3=−12+i√32
- ω2=e−2πi/3=−12−i√32
1+ω+ω2=0
We are given two equations:
1. 1a+ω+1b+ω+1c+ω=2ω2
2. 1(a+ω)2+1(b+ω)2+1(c+ω)2=2ω
We can generalize the form:
1a+x+1b+x+1c+x=2x
for x=ω and x=ω2.
From the generalized form, we can derive:
3x2+2(a+b+c)x+(ab+ac+bc)(a+x)(b+x)(c+x)=2x
Cross-multiplying gives us:
3x3+2(a+b+c)x2+(ab+ac+bc)x−2abc=0
Since ω and ω2 are roots, let the third root be α. By Vieta's formulas:
α+ω+ω2=0⟹α=−(ω+ω2)=1
Now we substitute α=1 back into the polynomial:
1a+1+1b+1+1c+1
We need to evaluate:
1a+1+1b+1+1c+1
Using the same form we derived:
1a+x+1b+x+1c+x=2x
for x=1:
1a+1+1b+1+1c+1=2
Thus, the value of 1a+1+1b+1+1c+1 is:
2
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE3.1
4 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE3.2
9 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - ILLUSTRATION
110 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions
101 Videos
Similar Questions
If 1,ω,ω2 are three cube roots of unity, prove that
(1−ω)(1−ω2)=3
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1+ω2)4=ω
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1+ω−ω2)(1−ω+ω2)=4
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
11+ω+11+ω2=1
View SolutionIf ω be an imaginary cube root of unity, show that: 11+2ω+12+ω−11+ω=0.
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
ω28+ω29+1=0
View SolutionIf 1, ωandω2 are the cube roots of unity, prove that a+bω+cω2c+aω+bω2=ω2
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω−ω2)6=64
View SolutionIf 1,ω,ω2 are the cube roots of unity, then △
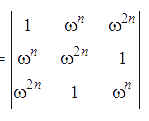
is equal to.....
View SolutionIf 1, ω and ω2 are the cube roots of unity evaluate (1−ω4+ω8)(1−ω8+ω16).
View Solution