Let 1,,w2 be the cube root of unity. The least possible degree of a polynomial with real coefficients having roots 2w,(2+3w),(2+3w2),(2−w−w2) is _____________.
The correct Answer is:5
Roots are 2ω,(2+3ω),(2+3ω2),(2−ω−ω2)
2+3ωand2+3ω2 are conjugate to each other.
2ω is complex root, then other root must be 2ω2 (as complex roots occur in conjugate pair)
2−ω−ω2=2−(−1)=3 which is real.
Hence, least degree of the polynomial is 5.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - ARCHIVES (SINGLE CORRECT ANSWER TYPE )11videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - LINKED COMPREHENSION TYPE36videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions101videos
CONIC SECTIONS
Similar Questions
Let 1,w,w2 be the cube root of unity. The least possible degree of a polynomial with real coefficients having roots 2w,(2+3w),(2+3w2),(2−w−w2) is _____________.
View SolutionLet I, ω and ω2 be the cube roots of unity. The least possible degree of a polynomial, with real coefficients having 2ω2,3+4ω,3+4ω2 and 5−ω−ω2 as roots is -
View Solution
Knowledge Check
- Question 1 - Select One
If 1,ω,ω2 are cube roots of unity then the value of (2+2ω−3ω2)3 is
A125B−125C27D−27
If 1,ω,ω2 are the cube roots of unity, then △
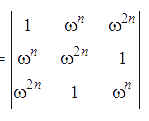
is equal to.....View SolutionIf ω is a cube root of unity, then
1+ω= …..View SolutionIf ω is a cube root of unity, then
ω3= ……View SolutionIf ω is a cube root of unity, then
ω+ω2=…..View SolutionIf ω is a cube root of unity, then
1+ω2= …..View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω)(1−ω2)=3View SolutionIf 1,ω,ω2 are cube roots of unity, prove that 1,ω,ω2 are vertices of an equilateral triangle
View Solution

