Match the conics in List I with the statements/expressions in List II


Video Solution
Text Solution
The correct Answer is:c→p,qs,t
c→p,q,s,t
Let a=3−3ω+2ω2
⇒aω=3ω−3ω2+2
⇒aω2=3ω2−3+2ω
Now given a4n+3(1+ω4n+3+(ω2)4n+3)=0
Thus, n should not be a mulitple of 3.
|
Topper's Solved these Questions
Similar Questions
Match the substances in List I with the appropriate answer in List II.

View SolutionMatch the statements in List I with the correct answer from List II.

View SolutionMatch the chemical reactions in List I with the appropriate answer in List II.

View SolutionMatch reactions written in List-I with their mechanism in List -II.

View SolutionMatch the salls in List-I with their use in List-II.

View SolutionMatch the separation of components in List I with the most appropriate process in List II.

View Solution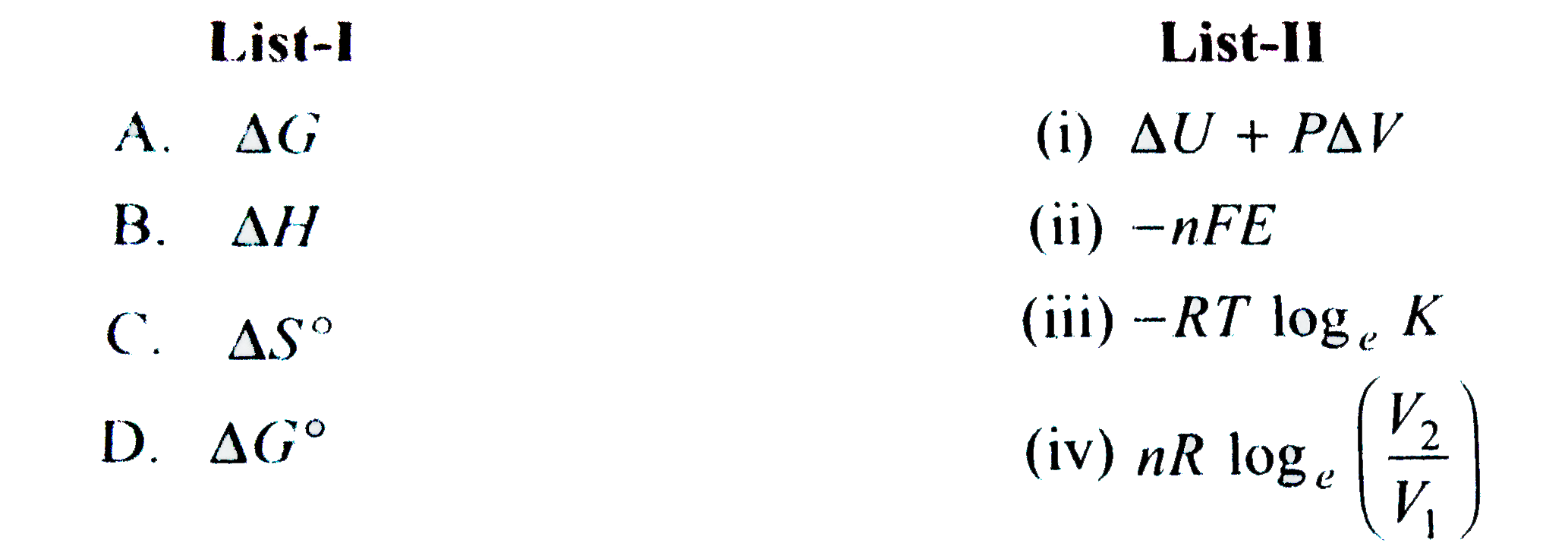 ltBrgt Match the physical changes in List-I with their relations given in List-II:
ltBrgt Match the physical changes in List-I with their relations given in List-II:
View SolutionMatch List I with List II

View SolutionMatch the compounds given in list I with their characterstics reactions in list II

View SolutionMatch the statements in List I the appropriate answer in List II.

View Solution
