Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.
The correct Answer is:64 and 4
Let the two numbers be a and b. Then,
A.M.=34
⇒a+b2=34 or a+b=68
G.M=16
⇒√ab=16 or ab=256
∴(a−b)2=(a+b)2−4ab
or (a−b)2=(68)2−4×256=3600
or a-b=60 (2)
On solving (1) and (2), we get a= 64 and b=4. Hence, the required numbers are 64 and 4.
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - CONCEPT APPLICATION EXERICISE 5.5
10 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - CONCEPT APPLICATION EXERICISE 5.6
11 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - CONCEPT APPLICATION EXERICISE 5.3
9 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
Similar Questions
Find two number whose arithmetic mean is 34 and the geometric mean is 16 .
View SolutionThe harmonic mean of two numbers is 4. Their arithmetic mean A and the geometric mean G satisfy the relation 2A+G2=27. Find two numbers.
View SolutionThe harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If 2A+G2=27,a+b=α and |a−b|=β, then the value of αβ is equal to
View SolutionFind the arithmetic mean of 4 and 12.
View SolutionFind the arithmetic mean of:
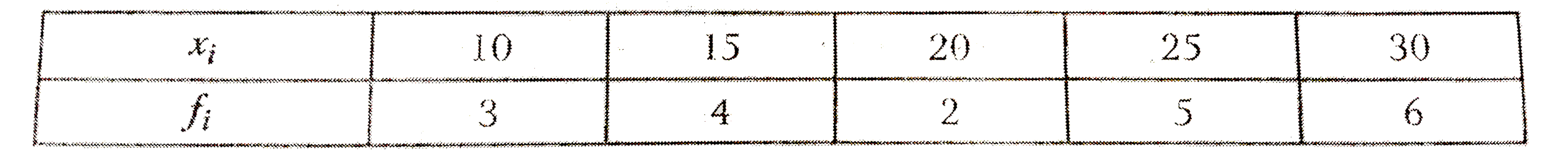
View SolutionLet two numbers have arithmatic mean 9 and geometric mean 4.Then these numbers are roots of the equation (a) x2+18x+16=0 (b) x2−18x−16=0 (c) x2+18x−16=0 (d) x2−18x+16=0
View SolutionFind the geometric mean of 12 and 27.
View SolutionFind the geometric mean of 6 and 24 .
View SolutionFind the sum of 12 numbers whose mean is 11.
View SolutionFind the single arithmetic mean between: 7and31
View Solution
