A person drops a ball from an 80 m tall building and each time the ball bounces, it rebounds to p% of its previous height. If the ball travels a total distance of 320 m, then the value of p is
The correct Answer is:60
To solve the problem, we need to determine the value of p given that a ball is dropped from a height of 80 meters and travels a total distance of 320 meters after bouncing back to p% of its previous height.
1. Understanding the Problem:
- The ball is dropped from a height of 80 meters.
- After each bounce, it rebounds to p% of the height from which it fell.
2. Distance Calculation:
- The initial drop distance is 80 meters.
- After the first bounce, the ball rises to p100×80 meters.
- It then falls the same distance, so the distance for the first bounce (up and down) is 2×p100×80.
3. Total Distance:
- The total distance traveled by the ball can be expressed as:
Total Distance=80+2(p100×80)+2(p21002×80)+2(p31003×80)+…
- This can be simplified to:
Total Distance=80+160(p100)+160(p21002)+160(p31003)+…
4. Recognizing the Series:
- The series 160(p100)+160(p21002)+160(p31003)+… is a geometric series with:
- First term a=160(p100)
- Common ratio r=p100
5. Sum of the Geometric Series:
- The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
- Therefore, the total distance becomes:
Total Distance=80+160(p100)1−(p100)
6. Setting Up the Equation:
- Given that the total distance is 320 meters, we can set up the equation:
320=80+160(p100)1−(p100)
- Simplifying this gives:
240=160(p100)1−(p100)
7. Cross Multiplying:
- Cross multiplying gives:
240(1−p100)=160(p100)
- Expanding this results in:
240−240p100=160p100
8. Combining Like Terms:
- Rearranging gives:
240=240p100+160p100
- This simplifies to:
240=400p100
9. Solving for p:
- Multiplying both sides by 100 gives:
24000=400p
- Dividing by 400 results in:
p=60
Final Answer:
The value of p is 60%.
- The ball is dropped from a height of 80 meters.
- After each bounce, it rebounds to p% of the height from which it fell.
- The initial drop distance is 80 meters.
- After the first bounce, the ball rises to p100×80 meters.
- It then falls the same distance, so the distance for the first bounce (up and down) is 2×p100×80.
- The total distance traveled by the ball can be expressed as:
Total Distance=80+2(p100×80)+2(p21002×80)+2(p31003×80)+…
- This can be simplified to:
Total Distance=80+160(p100)+160(p21002)+160(p31003)+…
- The series 160(p100)+160(p21002)+160(p31003)+… is a geometric series with:
- First term a=160(p100)
- Common ratio r=p100
- The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
- Therefore, the total distance becomes:
Total Distance=80+160(p100)1−(p100)
- Given that the total distance is 320 meters, we can set up the equation:
320=80+160(p100)1−(p100)
- Simplifying this gives:
240=160(p100)1−(p100)
- Cross multiplying gives:
240(1−p100)=160(p100)
- Expanding this results in:
240−240p100=160p100
- Rearranging gives:
240=240p100+160p100
- This simplifies to:
240=400p100
- Multiplying both sides by 100 gives:
24000=400p
- Dividing by 400 results in:
p=60
The value of p is 60%.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES ( JEE MAIN )(SINGLE CORRECT ANSWER TYPE )16videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES ( JEE ADVANCED )(SINGLE CORRECT ANSWER TYPE )3videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - EXERCIESE ( LINKED COMPREHENSION TYPE )60videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
Similar Questions
A golf ball is dropped from a height of 80 m. Each time the ball hits the ground, it rebounds to 1/3 of the height through which it has fallen. Then total distance travelled by the ball is 240m b. 160m c. 120m d. 320m
View SolutionTouching a hemispherical dome of radius R there is a vertical tower of height H=4r. A boy projects a ball horizontally at speed u from the top of the tower. The ball strikes the dome at a height R2 from ground and rebounds. After rebounding the ball retraces back its path into the hands of the boy. Then the value of u is :
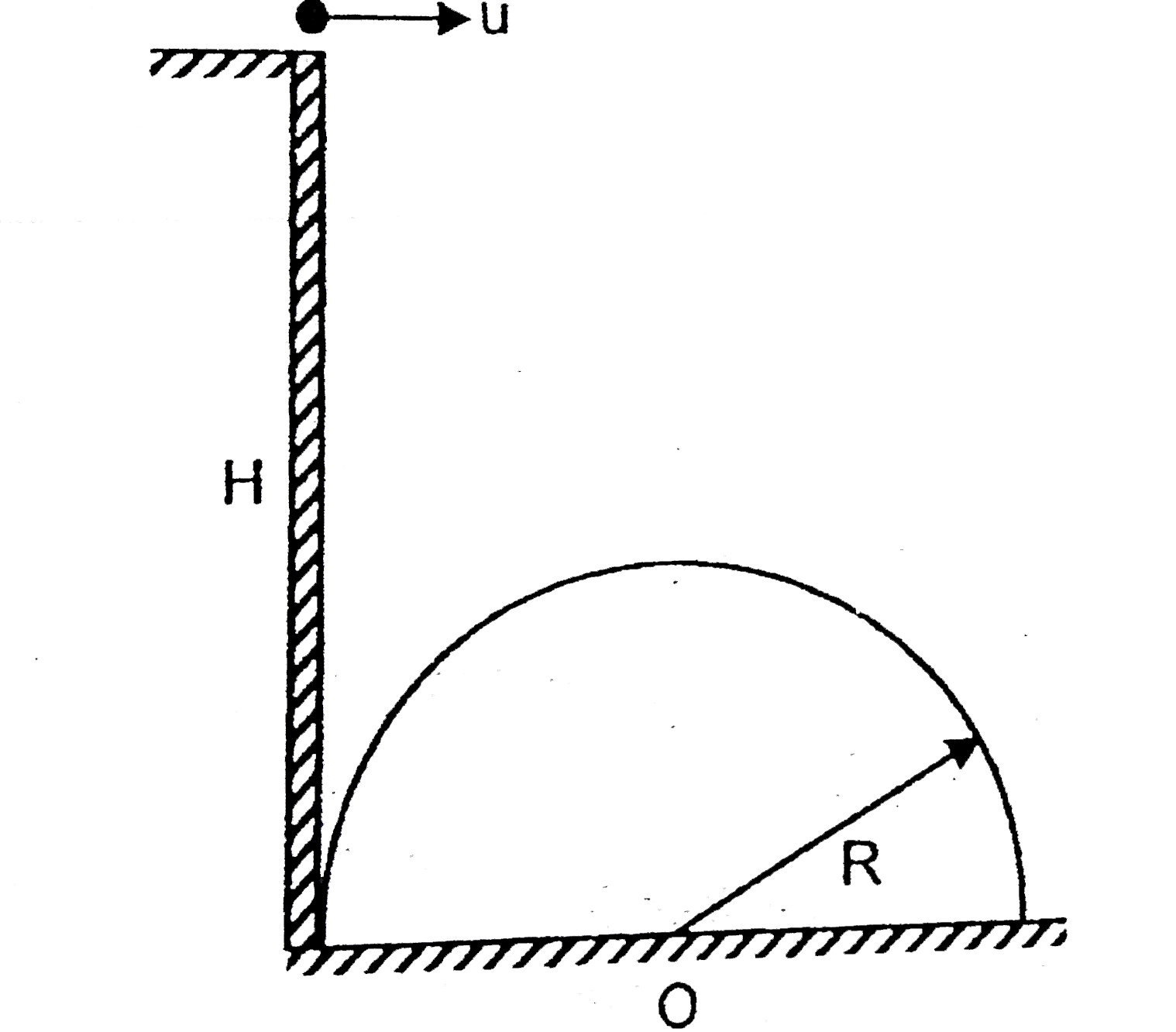 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball bounce of 80% of its original height . What fraction of its mechanical energy is lost in each bounce ?
A0.20B0.60C0.40D1
A ball of mass 1 kg falls from a height of 5 m above the free surface of water. The relative density of the solid ball is s=23. The ball travels a distance of 2 m under water and becomes stationary. The work done by the resistive forces of water is (−10n)J. Find value of n.
View SolutionA ball is dropped on the floor from a height of 10m. It rebounds to a height of 2.5 m if the ball is in contact with floor for 0.01 s then the average acceleration during contact is nearly
View SolutionA ball is dropped on the floor from a height of 10m. It rebounds to a height of 2.5 m if the ball is in contact with floor for 0.01 s then the average acceleration during contact is nearly
View SolutionA ball is dropped from height 10 m . Ball is embedded in sand 1 m and stops, then
View SolutionA steel ball is dropped from the roof of a building .An observer standing in front of a window 1.25 m high notes that the ball takes 1/8 s to fall from the top to the bottom of the window .The ball reappears at the bottom of the window 2s after passing it on the way down,if the collision between the ball reappears at the bottom of the window 2s after passing it on the way down.If the collision between the ball and the ground is perfectly elastic,then find the height of the building?Take g=10 m/s2.
View SolutionA ball is dropped onto a floor from a height of 10m. If 20% of its initial energy is lost,then the height of bounce is
View SolutionA ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. The relative speed of the balls varies with time as
View Solution

