Three distinct points P(3u2,2u3);Q(3v2,2v3) and R(3w2,2w3) are collinear then
The correct Answer is:0
∣∣
∣
∣∣3u22u313y22y313w22w31∣∣
∣
∣∣=0
R1→R1−R2 and R2→R2−R3
or ∣∣
∣
∣∣u2−v2u3−v30v2−w2v3−w30w2w31∣∣
∣
∣∣=0
or ∣∣
∣
∣∣u+vu2+v2+w0v+wv2+w20w2w31∣∣
∣
∣∣=0
R1→R1−R2
or ∣∣
∣
∣∣u−w(u2−w2)+v(u−w)0v+wv2+w2+vw0w2w31∣∣
∣
∣∣=0
or (v2+w2+vw)−(v+w)[(v+w)+u]=0
or v2+w2+vw−(v+w)2−u(v+w)=0
or uv+vw+wu=0
Topper's Solved these Questions
- DETERMINANTBook:CENGAGE ENGLISHChapter:DETERMINANTExercise:Multiple Correct Answer
Explore 5 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
Knowledge Check
20u3v6(2)−15u2v10u4v+30u3v3
Which of the following is the reduced form of the expression above?A5uv40u7v4B2v−1u+2uv2C4uv−32u2+2uv2D2uv−3uv2u2+6
Statement 1 : The chord of contact of the circle x2+y2=1 w.r.t. the points (2, 3), (3, 5), and (1, 1) are concurrent. Statement 2 : Points (1, 1), (2, 3), and (3, 5) are collinear.
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are
View SolutionIf A=⎛⎜⎝100210321⎞⎟⎠,U1,U2,andU3 are column matrices
satisfying AU1=⎛⎜⎝100⎞⎟⎠,AU2=⎛⎜⎝230⎞⎟⎠andAU3=⎛⎜⎝231⎞⎟⎠ and
U is 3×3 matrix when columns areU1,U2,U3 then
answer the following questions
The value of (3 2 0) U⎛⎜⎝320⎞⎟⎠ is
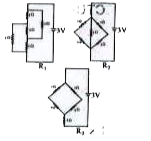
View SolutionFig shows three resistor configuration R1,R2andR3 connected to 3V battery. If the power dissipated by the configuration R1,R2andR3 is P1,P2andP3 respectively, then
View SolutionIf z1,z2,z3 and u,v,w are complex numbers represending the vertices of two triangles such that z3=(1−t)z1+tz2andw=(1−u)u+tv, where t is a complex number, then the two triangles
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionIf each pair of the three equations x2−p1x+q1=0,x2−p2c+q2=0,x2−p3x+q3=0 have common root, prove that, p21+p22+p23+4(q1+q2+q3)=2(p2p3+p3p1+p1p2)
View Solution