Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: (1) 25 (2) 30 (3) 12.5 (4) 10
30
12.5
10
25
The correct Answer is:4
Total length r+r+rθ=2θ
→θ=20−2rr ltbvrgt Therefore area of flower bed

A=12r2θ=12r220−2rr
→A=10r−r2=25−(r−5)2
∴Amax=25 (when r=5)
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension Type
2 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension type
50 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type
24 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
A wire of length 20m is available to fence off a flower bed in the form of a sector of a circle. What must be the radius of the circle, if we wish to have a flower bed with the greatest possible area?
View SolutionIn Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
View SolutionFind maximum possible area that can be enclosed by a wire of length 20cm by bending it in form of a circular sector. 10 (b) 25 (c) 30 (d) 20
View SolutionIf one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0 , is a chord of a circle S, whose centre is at (−3,2) , then the radius of S is : (1) 5√2 (2) 5√3 (3) 5 (4) 10
View SolutionThe shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn there are flower-beds having a uniform width of 2 m.
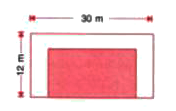
Hence, or otherwise, find the area of the flower- beds.
View SolutionMaximum possible area that can be enclosed by a wire of length 20 cm by bending it in form of a circular sector is 10 b. 25 c. 30 d. 20
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionIf the mid-point of a chord of the ellipse x216+y225=1 (0, 3), then length of the chord is (1) 325 (2) 16 (3) 45 12 (4) 32
View SolutionA circular flower bed is surrounded by a path 4m wide. The diameter of the flower bed is 66m. What is the area of this path ? (π=3.14)
View Solution
