Verify assoiativity for the following three mappings : f:N→Z0 (the set of non zero integers), g:Z0→Q and h:Q→R given by f(x)=2x,g(x)=1x and h(x)=ex.
Step by step video & image solution for Verify assoiativity for the following three mappings : f: N->Z_0 (the set of non zero integers), g: Z_0->Q and h: Q->R given by f(x)=2x ,g(x)=1/x and h(x)=e^xdot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Verify assoiativity for the following three mappings : f:N→Z0 (the set of non zero integers), g:Z0→Z and h:Q→R given by f(x)=2x,g(x)=1x and h(x)=ex.
View SolutionCheck the injectivity and surjectivity of the following functions:
(i) f:N→Ngiven by f(x)=x2
(ii) f:Z→Zgiven by f(x)=x2
(iii) f:R→Rgiven by f(x)=x2
(iv) f:N→Ngiven by f(x)=x3
(v) f:Z→Z given by f(x)=x3
View SolutionIf ∫sinxd(secx)=f(x)−g(x)+c,then f(x)=secx (b) f(x)=tanx g(x)=2x (d) g(x)=x
View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
View SolutionLe f:[0, ∞)→R and g:R→R be defined by f(x)=√x and g(x)=x. Find f+g, f−g, fg andfg.
View SolutionIf f:R→R,g,R→R be two funcitons, and h(x)=2min{f(x)−g(x),0} then h(x)=
View SolutionIf f,g, h are three functions defined from R → R as follows: Find the range of f(x)=x2
View SolutionIf f:R→Randg:R→R are two mappings such that f(x)=2xandg(x)=x2+2 then find fogandgog.
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
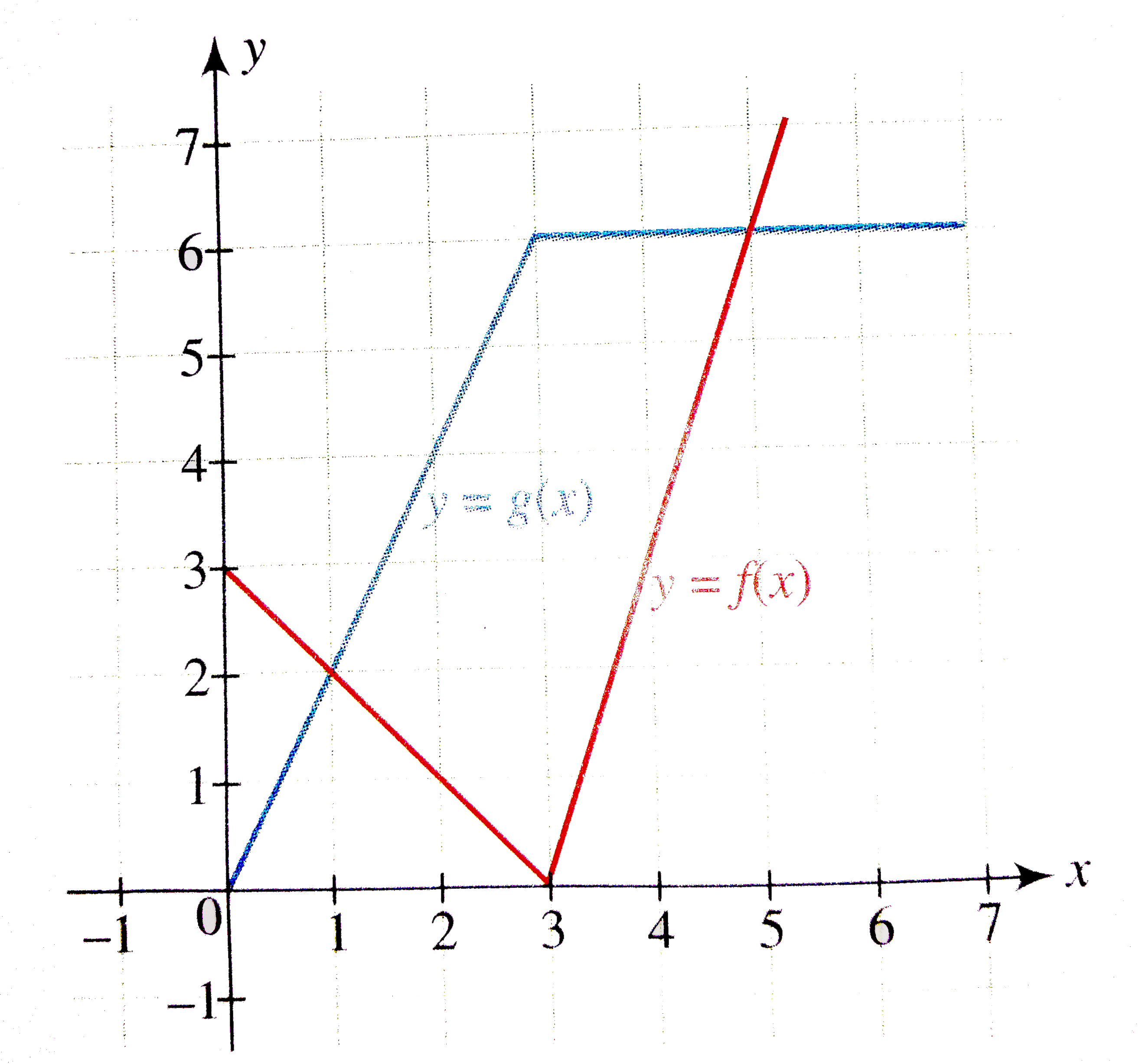
View Solution
