If f(x)=⎧⎪⎨⎪⎩ax2+b0≤x<14x=1x+31<x≥2⎞⎟⎠ then the value of(a,b) for which f(x) cannot be continuous at x=1, is (a)(2,2) (b) (3,1)(c)(4,0) (d)(5,2)
To determine the values of (a,b) for which the function f(x) is not continuous at x=1, we will analyze the function piecewise and check the conditions for continuity.
1. Define the Function:
The function is given as:
f(x)=⎧⎨⎩ax2+bif 0≤x<14if x=1x+3if 1<x≤2
2. Check Continuity at x=1:
For f(x) to be continuous at x=1, the following condition must hold:
limx→1−f(x)=f(1)=limx→1+f(x)
3. Calculate limx→1−f(x):
For x approaching 1 from the left, we use the first piece of the function:
limx→1−f(x)=limx→1−(ax2+b)=a(1)2+b=a+b
4. Calculate f(1):
From the definition of the function, we have:
f(1)=4
5. Calculate limx→1+f(x):
For x approaching 1 from the right, we use the second piece of the function:
limx→1+f(x)=limx→1+(x+3)=1+3=4
6. Set Up the Continuity Condition:
For continuity at x=1, we set:
a+b=4
7. Determine Conditions for Discontinuity:
The function will be discontinuous at x=1 if:
a+b≠4
8. Evaluate Given Options:
Now we will evaluate the options provided to find pairs (a,b) such that a+b≠4:
- (a) (2,2): 2+2=4 (Continuous)
- (b) (3,1): 3+1=4 (Continuous)
- (c) (4,0): 4+0=4 (Continuous)
- (d) (5,2): 5+2=7 (Discontinuous)
9. Conclusion:
The only pair (a,b) for which f(x) cannot be continuous at x=1 is:
(5,2)
The function is given as:
f(x)=⎧⎨⎩ax2+bif 0≤x<14if x=1x+3if 1<x≤2
For f(x) to be continuous at x=1, the following condition must hold:
limx→1−f(x)=f(1)=limx→1+f(x)
For x approaching 1 from the left, we use the first piece of the function:
limx→1−f(x)=limx→1−(ax2+b)=a(1)2+b=a+b
From the definition of the function, we have:
f(1)=4
For x approaching 1 from the right, we use the second piece of the function:
limx→1+f(x)=limx→1+(x+3)=1+3=4
For continuity at x=1, we set:
a+b=4
The function will be discontinuous at x=1 if:
a+b≠4
Now we will evaluate the options provided to find pairs (a,b) such that a+b≠4:
- (a) (2,2): 2+2=4 (Continuous)
- (b) (3,1): 3+1=4 (Continuous)
- (c) (4,0): 4+0=4 (Continuous)
- (d) (5,2): 5+2=7 (Discontinuous)
The only pair (a,b) for which f(x) cannot be continuous at x=1 is:
(5,2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
If f(x)=ax2+bx+c,a≠0 and a, b , and c are all negative , which could be the graph of f(x) ?
A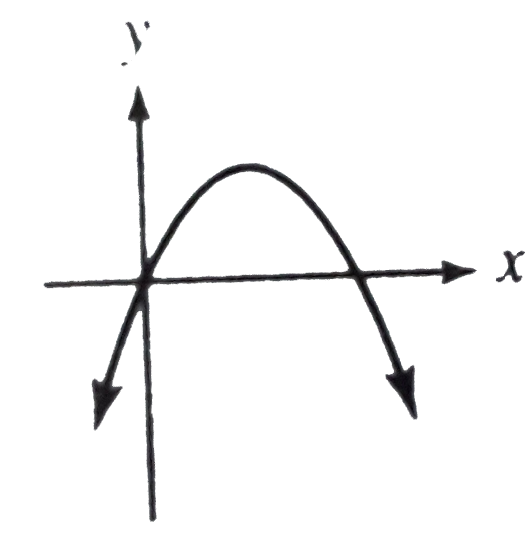 B
B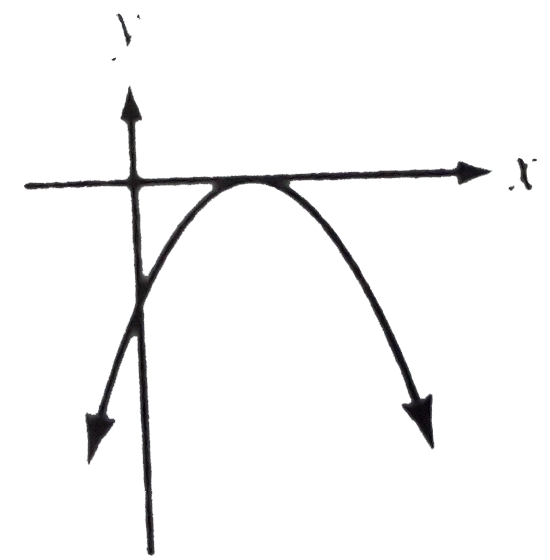 C
C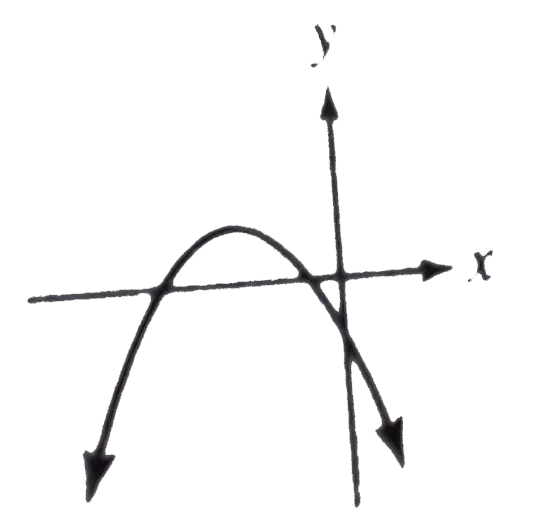 D
D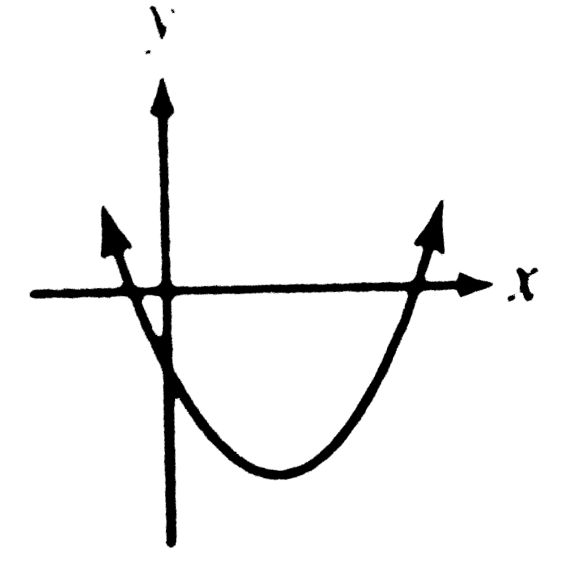
Find the values of a and b so that the function f(x) defined by f(x)={(x^2 +ax+b),(0<=x<2),(3x+2) , (2<=x<=4), (2a x+5b), (4 < x <= 8)} becomes continuous on [0,pi].
View SolutionFind the value of 'a' and 'b' limx→2andlimx→4 exists where
f(x)⎧⎪⎨⎪⎩x2+ax+b0≤x<23x+22≤x≤42ax+5b4<x≤8
View SolutionIf f(x)=⎧⎪⎨⎪⎩1+x,−1≤x<0x2−1,0<x<22x,2≤x
Find f(3),f(−2),f(0),f(12)f(2−h),f(−1+h), where h>0 is very small.
View SolutionLet f(x)=ax2+bx+c,a≠0, such the f(−1−x)=f(−1+x)∀x∈R. Also given that f(x)=0 has no real roots and 4a+b>0.
Let p=b−4a,q=2a+b, then pq is:
View Solutionfind the values of a and b , such that f(x)={ax2+1,x≤1andx2+ax+b,x>1 is differentiable at x=1
View Solutionlet f(x)={x2x≤0axx>0 then f (x) is derivable at x = 0 if
View SolutionLet f(x) be defined in the interval [0,4] such that
f(x)=⎧⎪⎨⎪⎩1−x0≤x≤1x+21<x<24−x2≤x≤4 , then the number of points where f(x) is discontinuous is (a) 1 (b) 2 (c) 3 (d) none of these
View Solution