In Figure, equal chords AB and CD of a circle with centre O, cut at right angles at E. If M and N are mid-point of AB and CD respectively, prove that OMEN is a square.
To prove that quadrilateral OMEN is a square, we will follow these steps:
Step 1: Identify the Given Information
We are given that:
- Chords AB and CD are equal and intersect at point E at right angles.
- M is the midpoint of chord AB.
- N is the midpoint of chord CD.
- O is the center of the circle.
Step 2: Establish the Right Angles
Since the chords AB and CD intersect at right angles at point E, we have:
- ∠OMB = ∠OND = 90° (as given).
Step 3: Show that OM = ON
Since AB and CD are equal chords of the circle, they are equidistant from the center O. Therefore, we can conclude that:
- OM = ON (the distances from the center to the midpoints of equal chords are equal).
Step 4: Consider Triangles OME and ONE
We will now consider triangles OME and ONE:
- OM = ON (from Step 3).
- OE = OE (common side).
- ∠OME = ∠ONE = 90° (from Step 2).
Step 5: Prove the Congruence of Triangles
Using the Side-Angle-Side (SAS) criterion for triangle congruence:
- Triangle OME ≅ Triangle ONE.
Step 6: Conclude that NE = ME
From the congruence of triangles OME and ONE, we can conclude:
- ME = NE (corresponding parts of congruent triangles are equal).
Step 7: Show that OMEN is a Quadrilateral
Now we have:
- OM = ON (from Step 3).
- ME = NE (from Step 6).
- ∠OME = ∠ONE = 90° (from Step 2).
This means that opposite sides are equal and angles are right angles, which indicates that OMEN is a parallelogram.
Step 8: Prove that OMEN is a Square
Since OM = ON and ME = NE, and we have right angles at O and E, we can conclude that:
- OMEN is a rectangle.
- Since OM = ON and ME = NE, it is also a rhombus.
Thus, OMEN is a square because it is both a rectangle and a rhombus.
Final Conclusion
Therefore, we have proved that quadrilateral OMEN is a square.
---
We are given that:
- Chords AB and CD are equal and intersect at point E at right angles.
- M is the midpoint of chord AB.
- N is the midpoint of chord CD.
- O is the center of the circle.
Since the chords AB and CD intersect at right angles at point E, we have:
- ∠OMB = ∠OND = 90° (as given).
Since AB and CD are equal chords of the circle, they are equidistant from the center O. Therefore, we can conclude that:
- OM = ON (the distances from the center to the midpoints of equal chords are equal).
We will now consider triangles OME and ONE:
- OM = ON (from Step 3).
- OE = OE (common side).
- ∠OME = ∠ONE = 90° (from Step 2).
Using the Side-Angle-Side (SAS) criterion for triangle congruence:
- Triangle OME ≅ Triangle ONE.
From the congruence of triangles OME and ONE, we can conclude:
- ME = NE (corresponding parts of congruent triangles are equal).
Now we have:
- OM = ON (from Step 3).
- ME = NE (from Step 6).
- ∠OME = ∠ONE = 90° (from Step 2).
Since OM = ON and ME = NE, and we have right angles at O and E, we can conclude that:
- OMEN is a rectangle.
- Since OM = ON and ME = NE, it is also a rhombus.
Therefore, we have proved that quadrilateral OMEN is a square.
Topper's Solved these Questions
Similar Questions
In Figure, equal chords AB and CD of a circle with centre O, cut at right angles at E. If M and N are mid-point of AB and CD respectively, prove that OMEN is a square.
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
View SolutionTwo equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
View SolutionIn Figure, if chords AB and CD of the circle intersect each other at right angles, then x+y= (a) 450 (b) 600 (c) 750 (d) 900
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, Prove that the points B, C, D and E are concyclic.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
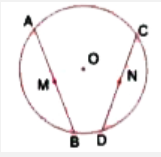
∠AMN=∠CNM.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :

(i) ∠BMN=∠DNM
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View Solution
