If h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
Step by step video & image solution for If h , c ,V are respectively the height, the curved surface and the volume of a cone, prove that 3piV h^3-C^2h^2+9V^2=0. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDERBOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDEREXERCISE - All Questions
133 Videos
- SURFACE AREA AND VOLUME OF A SPHERE BOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A SPHERE EXERCISE - All Questions
140 Videos
Similar Questions
Knowledge Check
V=13π(d2)2h
A circle of rubber with a constant diameter d is placed on a table, its perimeter is anchored to the table and a string is attached to its centre. When the string is pulled upwards, a cone is formed with height h and volume V. The relationship between d, h, and V is represented above. Which of the following statements must be true ?
I. As the volume of the cone decreases, the height also decreases.
II. If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by 3π.
III. If the height of the conc triples, the volume must also triple.AI onlyBI and II onlyCII and III onlyDI, II, and III
Show that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is 13h
View SolutionA solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h . If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is (a) 2h (b) 2h3 (c) 3h2 (d) 4h
View SolutionA solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h . If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is 2h (b) 2h3 (c) 3h2 (d) 4h
View SolutionIf the height and radius of a cone of volume V are doubled, then the volume of the cone, is (a) 3 V (b) 4 V (c) 6 V (d) 8 V
View SolutionThe area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
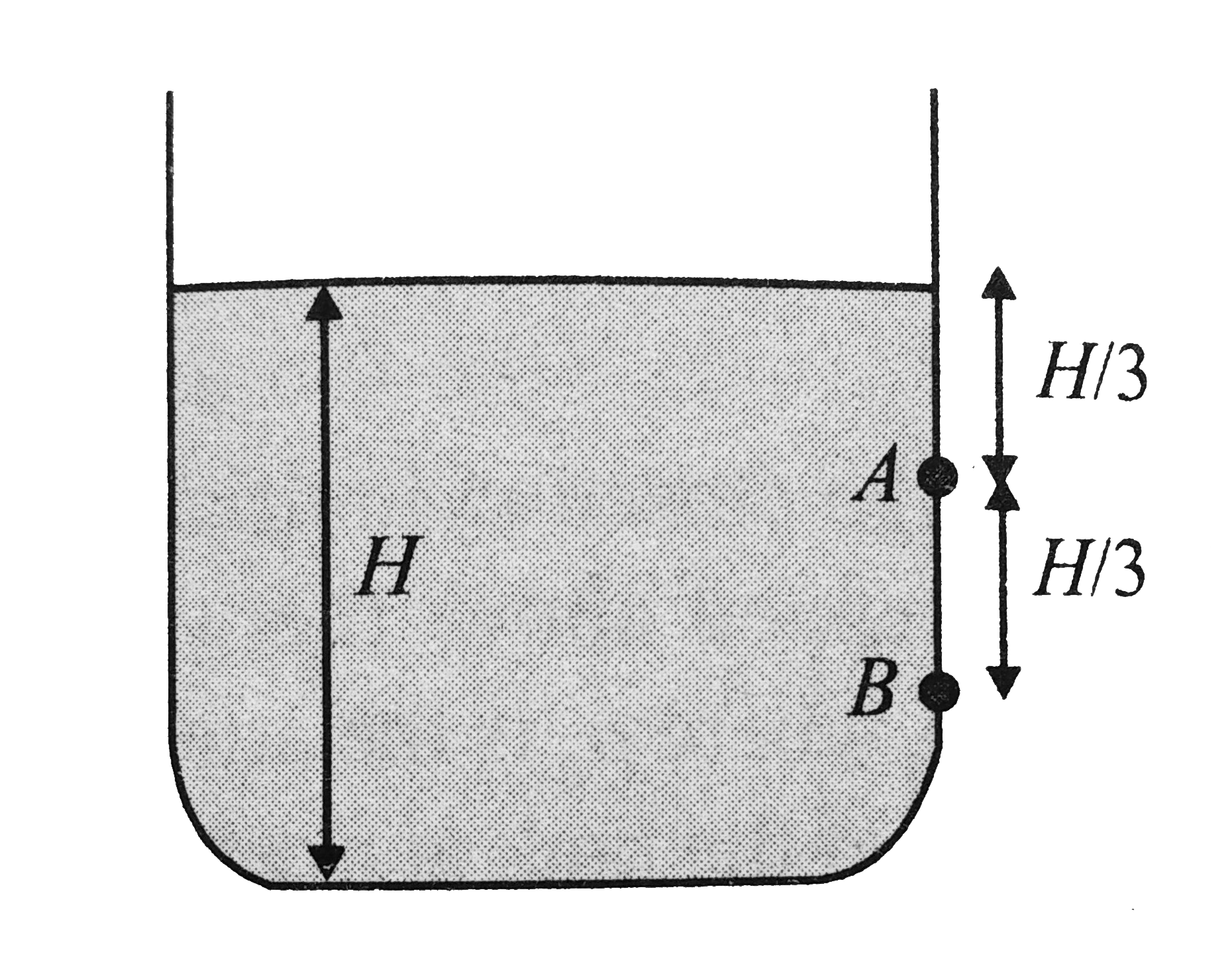
View SolutionFrom a given solid cone of height H, another inverted cone is carved whose height is h such that its volume is maximum. Then the ratio Hh is
View SolutionThe difference between the value of Cp of H2 and Cv of He will be
View Solution
