In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
To find the area of the shaded region in the given figure, we follow these steps:
Step 1: Identify the components of the shaded region
The shaded region is the area of the semicircle CDA minus the area of triangle ADC.
Step 2: Calculate the radius of the semicircle
Given that OA (which is the radius of the larger circle) = 7 cm, the radius (r1) of the semicircle CDA is:
r1=7 cm
Step 3: Calculate the area of the semicircle CDA
The area of a semicircle is given by the formula:
Area of semicircle=12πr2
Substituting the radius:
Area of semicircle=12π(7)2=12π(49)=49π2 cm2
Step 4: Calculate the area of triangle ADC
Triangle ADC is a right triangle where:
- OA = 7 cm (height)
- CD = 14 cm (base, as it is the diameter of the circle)
The area of triangle ADC is given by:
Area of triangle=12×base×height
Substituting the values:
Area of triangle=12×14×7=49 cm2
Step 5: Calculate the area of the shaded region
Now, we can find the area of the shaded region by subtracting the area of triangle ADC from the area of semicircle CDA:
Area of shaded region=Area of semicircle−Area of triangle
Substituting the areas we calculated:
Area of shaded region=49π2−49 cm2
Step 6: Simplify the expression
To express this in a numerical form, we can approximate π as 227 or 3.14:
Using π≈3.14:
Area of shaded region≈49×3.142−49
Calculating:
≈153.862−49
≈76.93−49
≈27.93 cm2
Thus, the area of the shaded region is approximately 27.93 cm2.
The shaded region is the area of the semicircle CDA minus the area of triangle ADC.
Given that OA (which is the radius of the larger circle) = 7 cm, the radius (r1) of the semicircle CDA is:
r1=7 cm
The area of a semicircle is given by the formula:
Area of semicircle=12πr2
Substituting the radius:
Area of semicircle=12π(7)2=12π(49)=49π2 cm2
Triangle ADC is a right triangle where:
- OA = 7 cm (height)
- CD = 14 cm (base, as it is the diameter of the circle)
Area of triangle=12×base×height
Substituting the values:
Area of triangle=12×14×7=49 cm2
Now, we can find the area of the shaded region by subtracting the area of triangle ADC from the area of semicircle CDA:
Area of shaded region=Area of semicircle−Area of triangle
Substituting the areas we calculated:
Area of shaded region=49π2−49 cm2
To express this in a numerical form, we can approximate π as 227 or 3.14:
Using π≈3.14:
Area of shaded region≈49×3.142−49
Calculating:
≈153.862−49
≈76.93−49
≈27.93 cm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
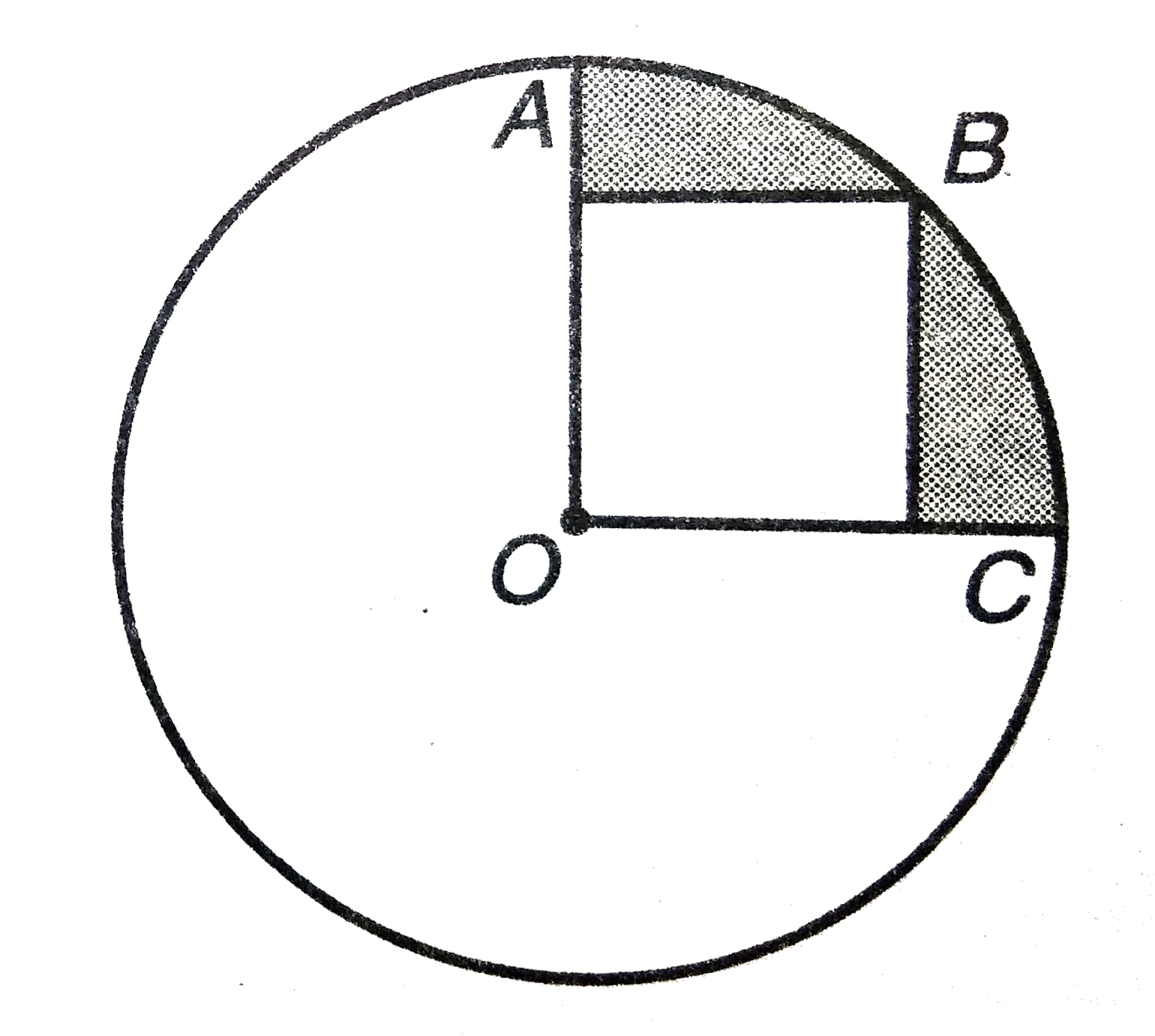
In the figure above, OABC is a square and B is a points on the circle with center O. If AB=6, what is the area of the shaded region?A9(π−2)B9(π−1)C12(π−2)D18(π−2)
Find the area of the shaded region in figure.

View SolutionFind the area of the shaded region in Figure.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
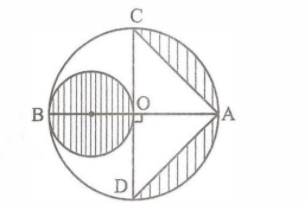
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn Figure -4 AB, and CD are two diameters of a circle with centre O perpendiclualr to each other and OD is the diameter of the circle . If OA = 7 cm , then find the carea of the shaded region .
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.

View SolutionIn Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View Solution


