The largest cone is curved out from one face of solid cube of side 21 cm find the volume of the remaining solid.
To find the volume of the remaining solid after a largest cone is carved out from one face of a solid cube with a side length of 21 cm, we will follow these steps:
Step 1: Calculate the volume of the cube.
The formula for the volume of a cube is given by:
Vcube=side3
Given that the side of the cube is 21 cm:
Vcube=213=21×21×21=9261 cm3
Step 2: Determine the dimensions of the cone.
The largest cone that can be carved out from one face of the cube will have:
- Radius r equal to half of the side of the cube.
- Height h equal to the side of the cube.
Calculating the radius:
r=212=10.5 cm
The height of the cone is:
h=21 cm
Step 3: Calculate the volume of the cone.
The formula for the volume of a cone is given by:
Vcone=13πr2h
Substituting the values of r and h:
Vcone=13π(10.5)2(21)
Calculating (10.5)2:
(10.5)2=110.25
Now substituting this back into the volume formula:
Vcone=13π(110.25)(21)
Calculating 110.25×21:
110.25×21=2315.25
Now substituting this value into the volume of the cone:
Vcone=13π(2315.25)
Using π≈3.14:
Vcone≈13×3.14×2315.25≈2425.5 cm3
Step 4: Calculate the volume of the remaining solid.
To find the volume of the remaining solid after carving out the cone, we subtract the volume of the cone from the volume of the cube:
Vremaining=Vcube−Vcone
Substituting the volumes we calculated:
Vremaining=9261−2425.5=6835.5 cm3
Final Answer:
The volume of the remaining solid is:
6835.5 cm3
The formula for the volume of a cube is given by:
Vcube=side3
Given that the side of the cube is 21 cm:
Vcube=213=21×21×21=9261 cm3
The largest cone that can be carved out from one face of the cube will have:
- Radius r equal to half of the side of the cube.
- Height h equal to the side of the cube.
r=212=10.5 cm
The height of the cone is:
h=21 cm
The formula for the volume of a cone is given by:
Vcone=13πr2h
Substituting the values of r and h:
Vcone=13π(10.5)2(21)
Calculating (10.5)2:
(10.5)2=110.25
Now substituting this back into the volume formula:
Vcone=13π(110.25)(21)
Calculating 110.25×21:
110.25×21=2315.25
Now substituting this value into the volume of the cone:
Vcone=13π(2315.25)
Using π≈3.14:
Vcone≈13×3.14×2315.25≈2425.5 cm3
To find the volume of the remaining solid after carving out the cone, we subtract the volume of the cone from the volume of the cube:
Vremaining=Vcube−Vcone
Substituting the volumes we calculated:
Vremaining=9261−2425.5=6835.5 cm3
The volume of the remaining solid is:
6835.5 cm3
Topper's Solved these Questions
Similar Questions
The largest possible sphere is carved out of a wooden solid cube of side 7cm. Find the volume of the wood left. (Useπ=227).
View SolutionThe largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
View SolutionThe largest sphere is carved out of a cube of a side 7 cm. Find the volume of the sphere.
View SolutionThe larges sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
View SolutionThe larges sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
View SolutionThe largest sphere is carved out of a cube of a side 7cm. Find the volume of the sphere.
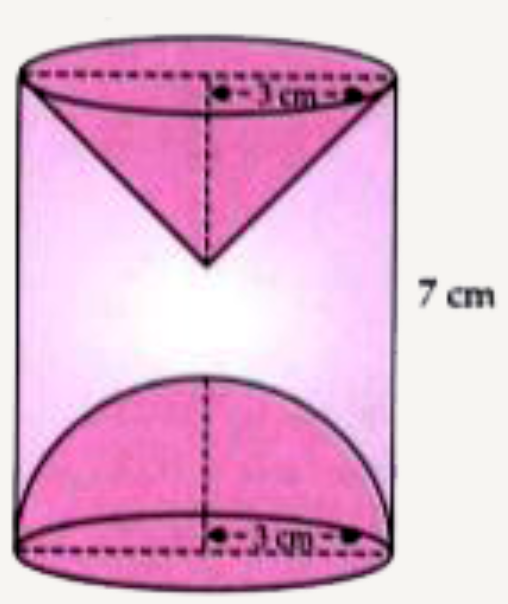
View SolutionA hemispherical and a conical hole is scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows :
The height of the solid cylinder is 7 cm, radius of each of hemisphere, come and cylinder is 3 cm. height of cone is 3 cm.
Give your answer correct to the nearest whole number.
(Take π=227)
View SolutionA hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
View SolutionHow many cubes of side 2 cm can be made from a solid cube of side 10 cm ?
View SolutionFrom a solid wooden cylinder of height 28 cm and diameter 6 cm, two conical cavities are hollowed out. The diameters of the cones are also of 6 cm and height 10.5 cm. Taking π=227 find the volume of the remaining solid.
View Solution
