Following is the age distribution of a group of students. Draw the cumulative frequency polygon, cumulative frequency curve (less than type) and hence obtain the median value.
To solve the problem of drawing the cumulative frequency polygon, cumulative frequency curve (less than type), and finding the median from the age distribution of a group of students, we will follow these steps:
Step 1: Organize the Data
Create a frequency distribution table for the age groups. The age groups and their corresponding frequencies are given.
| Age Group | Frequency |
|-----------|-----------|
| 5 - 6 | 40 |
| 6 - 7 | 56 |
| 7 - 8 | 60 |
| 8 - 9 | 66 |
| 9 - 10 | 72 |
| 10 - 11 | 96 |
| 11 - 12 | 98 |
| 12 - 13 | 74 |
| 13 - 14 | 64 |
| 14 - 15 | 46 |
| 15 - 16 | 20 |
| 16 - 17 | 10 |
Step 2: Create the Cumulative Frequency Table
Calculate the cumulative frequency (cf) for each age group. The cumulative frequency is obtained by adding the frequency of the current age group to the cumulative frequency of the previous age group.
| Age Group | Frequency | Cumulative Frequency (cf) |
|-----------|-----------|---------------------------|
| 5 - 6 | 40 | 40 |
| 6 - 7 | 56 | 96 |
| 7 - 8 | 60 | 156 |
| 8 - 9 | 66 | 222 |
| 9 - 10 | 72 | 294 |
| 10 - 11 | 96 | 390 |
| 11 - 12 | 98 | 488 |
| 12 - 13 | 74 | 562 |
| 13 - 14 | 64 | 626 |
| 14 - 15 | 46 | 672 |
| 15 - 16 | 20 | 692 |
| 16 - 17 | 10 | 702 |
Step 3: Prepare for the Cumulative Frequency Polygon
To draw the cumulative frequency polygon, we need to create a new table that includes the upper class limits and their corresponding cumulative frequencies.
| Age (Less than) | Cumulative Frequency (cf) |
|------------------|---------------------------|
| 6 | 40 |
| 7 | 96 |
| 8 | 156 |
| 9 | 222 |
| 10 | 294 |
| 11 | 390 |
| 12 | 488 |
| 13 | 562 |
| 14 | 626 |
| 15 | 672 |
| 16 | 692 |
| 17 | 702 |
Step 4: Plot the Cumulative Frequency Polygon
On a graph, plot the points from the table above with the age (less than) on the x-axis and the cumulative frequency on the y-axis. Connect the points with straight lines to form the cumulative frequency polygon.
Step 5: Draw the Cumulative Frequency Curve
The cumulative frequency curve is simply a smooth curve that connects the points plotted in the cumulative frequency polygon.
Step 6: Find the Median
To find the median, we need to calculate n/2 where n is the total number of students.
Total n=702
So, n/2=702/2=351.
Now, we look for the cumulative frequency that is just greater than or equal to 351 in our cumulative frequency table.
From the table, we see that 351 lies between the cumulative frequencies of 294 (for age 10) and 390 (for age 11).
To find the median, we can use linear interpolation:
Median = L + (n/2−cff)×c
Where:
- L = lower boundary of the median class (10)
- cf = cumulative frequency of the class before the median class (294)
- f = frequency of the median class (96)
- c = class width (1)
Substituting the values:
Median = 10 + (351−29496)×1
Median = 10 + (5796)
Median = 10 + 0.59375
Median = 10.59375
Final Answer
The median age of the group of students is approximately 10.59 years.
---
Create a frequency distribution table for the age groups. The age groups and their corresponding frequencies are given.
|-----------|-----------|
| 5 - 6 | 40 |
| 6 - 7 | 56 |
| 7 - 8 | 60 |
| 8 - 9 | 66 |
| 9 - 10 | 72 |
| 10 - 11 | 96 |
| 11 - 12 | 98 |
| 12 - 13 | 74 |
| 13 - 14 | 64 |
| 14 - 15 | 46 |
| 15 - 16 | 20 |
| 16 - 17 | 10 |
Calculate the cumulative frequency (cf) for each age group. The cumulative frequency is obtained by adding the frequency of the current age group to the cumulative frequency of the previous age group.
|-----------|-----------|---------------------------|
| 5 - 6 | 40 | 40 |
| 6 - 7 | 56 | 96 |
| 7 - 8 | 60 | 156 |
| 8 - 9 | 66 | 222 |
| 9 - 10 | 72 | 294 |
| 10 - 11 | 96 | 390 |
| 11 - 12 | 98 | 488 |
| 12 - 13 | 74 | 562 |
| 13 - 14 | 64 | 626 |
| 14 - 15 | 46 | 672 |
| 15 - 16 | 20 | 692 |
| 16 - 17 | 10 | 702 |
To draw the cumulative frequency polygon, we need to create a new table that includes the upper class limits and their corresponding cumulative frequencies.
|------------------|---------------------------|
| 6 | 40 |
| 7 | 96 |
| 8 | 156 |
| 9 | 222 |
| 10 | 294 |
| 11 | 390 |
| 12 | 488 |
| 13 | 562 |
| 14 | 626 |
| 15 | 672 |
| 16 | 692 |
| 17 | 702 |
On a graph, plot the points from the table above with the age (less than) on the x-axis and the cumulative frequency on the y-axis. Connect the points with straight lines to form the cumulative frequency polygon.
The cumulative frequency curve is simply a smooth curve that connects the points plotted in the cumulative frequency polygon.
To find the median, we need to calculate n/2 where n is the total number of students.
- L = lower boundary of the median class (10)
- cf = cumulative frequency of the class before the median class (294)
- f = frequency of the median class (96)
- c = class width (1)
The median age of the group of students is approximately 10.59 years.
Topper's Solved these Questions
Similar Questions
The following observations relate to the height of a group of persons. Draw the two types of cumulative frequency polygons and cumulative frequency curves and determine the median. Height in cms Frequency 140-143 143-146 146-149 149-152 152-155 155-158 158-161 161-164 164-167 167-170 170-173 173-176 176-179 179-182 3 9 26 31 45 64 78 85 96 72 60 43 20 6
View SolutionCumulative Frequency Distribution
View Solution
Knowledge Check
The cumulative frequency proceeding to the median class for the following data is
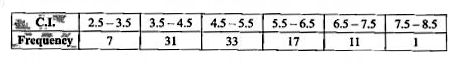 A71B88C38D40
A71B88C38D40
The following is the distribution of weights (in kg) of 40 persons.

Construct a cumulative frequency distribution (of the less than type) table for the data above.
View SolutionDraw a frequency polygon from the following frequency distribution

View SolutionThe following table shows the distribution of heights of a group of factory workers.

Determine the cumulative frequencies.
View SolutionDraw a frequency polygon from the following data:
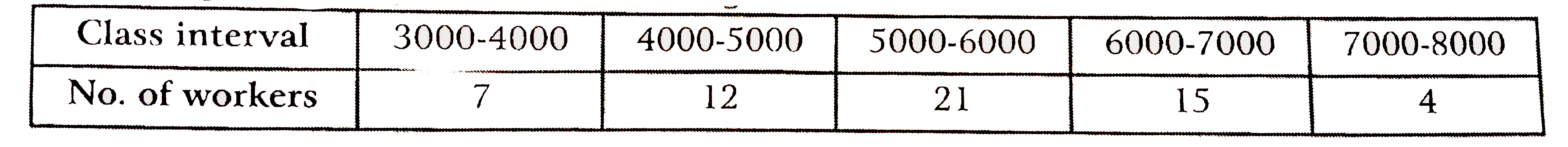
View SolutionThe following table shows the distribution of the heights of a group of factory workers :
Draw the 'less than' cumulative frequency curve on graph paper . Use 2 cm = 5 cm height on one axis and 2 cm = 10 workers on the other
Ht. (cm): 150−155155−160160−165165−170170−175175−180180−185 No. of workers 6 12 18 20 13 8 6
View SolutionIn a frequency distribution, ogives are graphical representation of (a) Frequency (b) Relative frequency (c) Cumulative frequency (d) Raw data
View SolutionExplain the difference between a frequency distribution and a cumulative frequency distribution.
View Solution