The angry Arjun carried some arrows for fighting with Bheeshm. With half the arrows, he cut down the arrows thrown by Bheeshm on him and with six other arrows he killed the rath driver of Bheeshm. With one arrow each he knocked down respectively the rath, flag and the bow of Bheeshm. Finally, with one more than four times the square root of arrows he laid Bheeshm unconscious on an arrow bed. Find the total number of arrows Arjun had.
To solve the problem, we will follow these steps:
1. Define the variable: Let the total number of arrows Arjun had be x.
2. Break down the information:
- Half of the arrows: x2
- Arrows used to kill the rath driver: 6
- Arrows used to knock down the rath, flag, and bow: 3 (1 for each)
- The final action: Arjun used 1+4√x arrows to lay Bheeshm unconscious.
3. Set up the equation:
The total number of arrows used can be expressed as:
x2+6+3+(1+4√x)=x
4. Simplify the equation:
Combine the constants:
x2+10+4√x=x
5. Rearrange the equation:
Move all terms to one side:
10+4√x=x−x2
This simplifies to:
10+4√x=x2
6. Multiply through by 2 to eliminate the fraction:
20+8√x=x
7. Rearrange the equation:
x−8√x−20=0
8. Let y=√x, then x=y2:
y2−8y−20=0
9. Use the quadratic formula:
The quadratic formula is given by:
y=−b±√b2−4ac2a
Here, a=1,b=−8,c=−20:
y=8±√(−8)2−4⋅1⋅(−20)2⋅1
y=8±√64+802
y=8±√1442
y=8±122
10. Calculate the values for y:
y=202=10ory=−42=−2
Since y must be non-negative, we take y=10.
11. Find x:
√x=10⟹x=102=100
12. Conclusion: The total number of arrows Arjun had is 100.
- Half of the arrows: x2
- Arrows used to kill the rath driver: 6
- Arrows used to knock down the rath, flag, and bow: 3 (1 for each)
- The final action: Arjun used 1+4√x arrows to lay Bheeshm unconscious.
The total number of arrows used can be expressed as:
x2+6+3+(1+4√x)=x
Combine the constants:
x2+10+4√x=x
Move all terms to one side:
10+4√x=x−x2
This simplifies to:
10+4√x=x2
20+8√x=x
x−8√x−20=0
y2−8y−20=0
The quadratic formula is given by:
y=−b±√b2−4ac2a
Here, a=1,b=−8,c=−20:
y=8±√(−8)2−4⋅1⋅(−20)2⋅1
y=8±√64+802
y=8±√1442
y=8±122
y=202=10ory=−42=−2
Since y must be non-negative, we take y=10.
√x=10⟹x=102=100
Topper's Solved these Questions
Similar Questions
What does the arrow drawn on a ray of light indicate?
View SolutionA uniformly thick plate in the shape of an arrow head has dimensions as shown. Find the distance of centre of mass from point O (in cm)

View SolutionIn transistor symbols, the arrows shows shows the direction of-
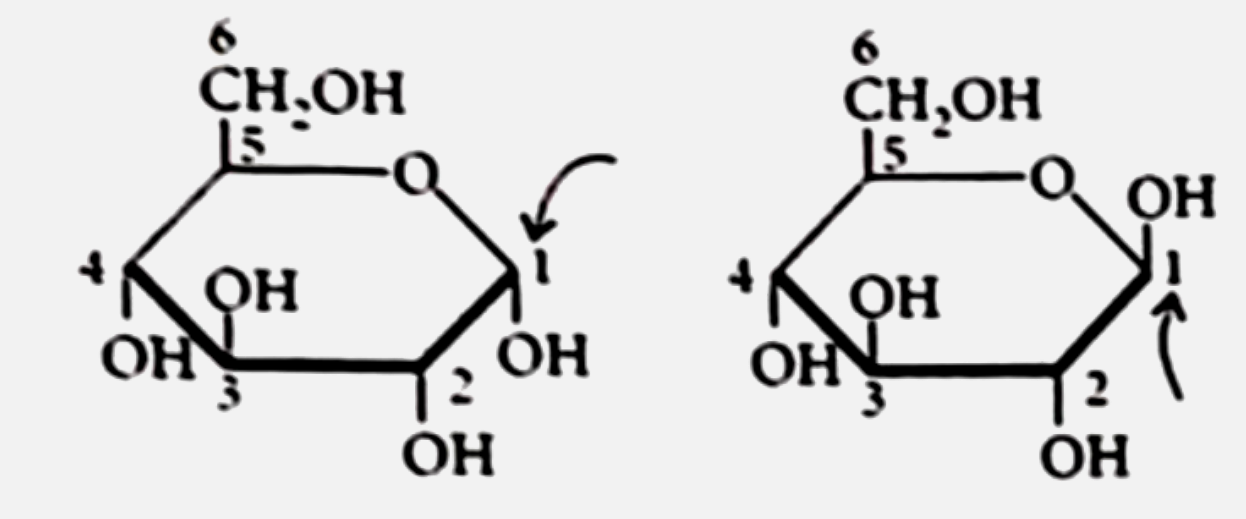
View SolutionWhat is the relationship between the given structures (look at the arrow)?
View SolutionAn arrow is shot in air, its time of flight is 5 sec and horizontal range is 200 m. the inclination of the arrow with the horizontal is
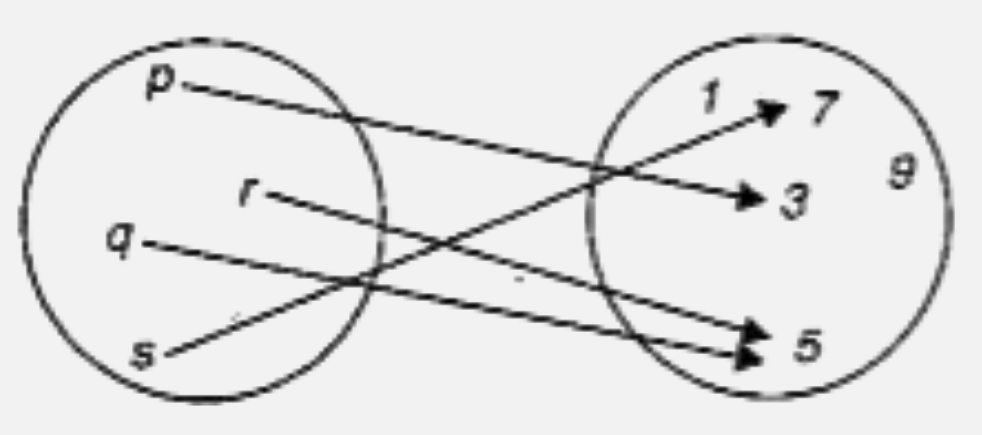
View SolutionWrite down the relation shown by the arrow diagram, by listing the ordered pairs. State the domain, co-domain, and the range of the relation.
View SolutionDraw a circuit diagram for a bulb connected to a cell with a switch. Mark arrows in the diagram to indicate the direction of flow of current.
View SolutionPredict the polarity of the capacitor when the two magnets are quickly moved in the directions marked by arrows.

View SolutionAn outline sketch of a tree is shown in the diagram below. Study the same and answer the question that follo:

What does the direction of arrows in B and C indicate?
View SolutionWhat kind of energy does a tightly drawn bow and arrow have?
View Solution
