Find the value of p , the mean of the following distribution is 7.5 x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
To find the value of p in the given distribution, we need to follow these steps:
Step 1: Set up the data
We have the following data:
- x: 3, 5, 7, 9, 11, 13
- f: 6, 8, 15, p, 8, 4
Step 2: Create the table for xi and fi
We will calculate xifi for each value of x and its corresponding frequency f.
| xi | fi | xifi |
|-----------|-----------|----------------|
| 3 | 6 | 3×6=18 |
| 5 | 8 | 5×8=40 |
| 7 | 15 | 7×15=105 |
| 9 | p | 9×p=9p |
| 11 | 8 | 11×8=88 |
| 13 | 4 | 13×4=52 |
Step 3: Calculate ∑fi and ∑fixi
Now we will sum the frequencies and the products:
- ∑fi=6+8+15+p+8+4=41+p
- ∑fixi=18+40+105+9p+88+52=303+9p
Step 4: Set up the equation for the mean
We know that the mean ¯x is given by:
¯x=∑fixi∑fi
Given that the mean is 7.5, we can set up the equation:
7.5=303+9p41+p
Step 5: Cross-multiply to eliminate the fraction
Cross-multiplying gives us:
7.5(41+p)=303+9p
Step 6: Distribute and simplify
Expanding the left side:
307.5+7.5p=303+9p
Step 7: Rearranging the equation
Rearranging gives us:
307.5−303=9p−7.5p
This simplifies to:
4.5=1.5p
Step 8: Solve for p
Dividing both sides by 1.5:
p=4.51.5=3
Conclusion
Thus, the value of p is 3.
---
We have the following data:
- f: 6, 8, 15, p, 8, 4
We will calculate xifi for each value of x and its corresponding frequency f.
|-----------|-----------|----------------|
| 3 | 6 | 3×6=18 |
| 5 | 8 | 5×8=40 |
| 7 | 15 | 7×15=105 |
| 9 | p | 9×p=9p |
| 11 | 8 | 11×8=88 |
| 13 | 4 | 13×4=52 |
Now we will sum the frequencies and the products:
- ∑fixi=18+40+105+9p+88+52=303+9p
We know that the mean ¯x is given by:
Cross-multiplying gives us:
Expanding the left side:
Rearranging gives us:
Dividing both sides by 1.5:
Thus, the value of p is 3.
Topper's Solved these Questions
Similar Questions
Find the value of P if the mean of the following distribution is 7.5

View SolutionFind the value of p, if the mean of the following distribution is 7.5. x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of if the mean of the following distribution is 7.5
View SolutionFind the value of p if the mean of the following distribution is 7.5. 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p, if mean of the following distribution is 7.5.
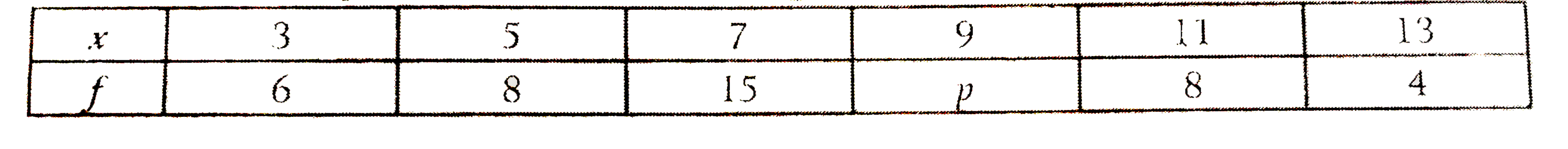
View SolutionFind the value of p, if the mean of the following distribution is 20 15 17 19 23 2 3 4 5 6
View SolutionFind the mean of the following distribution: x: 10 30 50 70 89 f: 7 8 10 15 10
View SolutionFind the mean of the following distribution: x: 4 6 9 10 15 f: 5 10 10 7 8
View SolutionFind the mean of the following distribution:
x: 4 6 9 10 15
f: 5 10 10 7 8
View SolutionFind the mean of the following distribution: x: 4 6 9 10 15 f: 5 10 10 7 8
View Solution
