Find the distance between the points: (i)P(−6,7) andQ(−1,−5) (ii)R(a+b,a−b) and S(a−b,−a−b) (iii)A(at1,2at1) and B(at2,2at2)
To find the distance between the given points, we will use the distance formula:
d=√(x2−x1)2+(y2−y1)2
where (x1,y1) and (x2,y2) are the coordinates of the two points.
(i) Find the distance between points P(-6, 7) and Q(-1, -5).
1. Identify the coordinates:
- P(−6,7) → x1=−6, y1=7
- Q(−1,−5) → x2=−1, y2=−5
2. Substitute the coordinates into the distance formula:
d=√((−1)−(−6))2+((−5)−7)2
3. Simplify the expressions:
- x2−x1=−1+6=5
- y2−y1=−5−7=−12
4. Substitute back into the formula:
d=√(5)2+(−12)2
5. Calculate the squares:
d=√25+144
6. Add the results:
d=√169
7. Take the square root:
d=13
(ii) Find the distance between points R(a+b, a-b) and S(a-b, -a-b).
1. Identify the coordinates:
- R(a+b,a−b) → x1=a+b, y1=a−b
- S(a−b,−a−b) → x2=a−b, y2=−a−b
2. Substitute the coordinates into the distance formula:
d=√((a−b)−(a+b))2+((−a−b)−(a−b))2
3. Simplify the expressions:
- x2−x1=(a−b)−(a+b)=−2b
- y2−y1=(−a−b)−(a−b)=−2a
4. Substitute back into the formula:
d=√(−2b)2+(−2a)2
5. Calculate the squares:
d=√4b2+4a2
6. Factor out the common term:
d=√4(a2+b2)=2√a2+b2
(iii) Find the distance between points A(at1, 2at1) and B(at2, 2at2).
1. Identify the coordinates:
- A(at1,2at1) → x1=at1, y1=2at1
- B(at2,2at2) → x2=at2, y2=2at2
2. Substitute the coordinates into the distance formula:
d=√(at2−at1)2+(2at2−2at1)2
3. Simplify the expressions:
- x2−x1=at2−at1=a(t2−t1)
- y2−y1=2at2−2at1=2a(t2−t1)
4. Substitute back into the formula:
d=√(a(t2−t1))2+(2a(t2−t1))2
5. Calculate the squares:
d=√a2(t2−t1)2+4a2(t2−t1)2
6. Factor out the common term:
d=√5a2(t2−t1)2=|t2−t1|⋅a√5
Summary of Solutions:
- (i) Distance between P and Q: 13
- (ii) Distance between R and S: 2√(a² + b²)
- (iii) Distance between A and B: |t₂ - t₁| a√5
- P(−6,7) → x1=−6, y1=7
- Q(−1,−5) → x2=−1, y2=−5
d=√((−1)−(−6))2+((−5)−7)2
- x2−x1=−1+6=5
- y2−y1=−5−7=−12
d=√(5)2+(−12)2
d=√25+144
d=√169
d=13
- R(a+b,a−b) → x1=a+b, y1=a−b
- S(a−b,−a−b) → x2=a−b, y2=−a−b
d=√((a−b)−(a+b))2+((−a−b)−(a−b))2
- x2−x1=(a−b)−(a+b)=−2b
- y2−y1=(−a−b)−(a−b)=−2a
d=√(−2b)2+(−2a)2
d=√4b2+4a2
d=√4(a2+b2)=2√a2+b2
- A(at1,2at1) → x1=at1, y1=2at1
- B(at2,2at2) → x2=at2, y2=2at2
d=√(at2−at1)2+(2at2−2at1)2
- x2−x1=at2−at1=a(t2−t1)
- y2−y1=2at2−2at1=2a(t2−t1)
d=√(a(t2−t1))2+(2a(t2−t1))2
d=√a2(t2−t1)2+4a2(t2−t1)2
d=√5a2(t2−t1)2=|t2−t1|⋅a√5
- (i) Distance between P and Q: 13
- (ii) Distance between R and S: 2√(a² + b²)
- (iii) Distance between A and B: |t₂ - t₁| a√5
Topper's Solved these Questions
Similar Questions
Find the distance between the following points : (i) A(−6,4)andB(2,−2) (ii) A(−5,−1)andB(0,4)
View SolutionFind the distance between the following pairs of points :
(i) (2,3),(4,1)
(ii) (–5,7),(–1,3)
(iii) (a,b),(–a,–b)
View SolutionFind the distance between the following pairs of points : (i) (2,3),(4,1) (ii) (−5,−7),(−1,3) (iii) (a,b),(−a,−b)
View SolutionFind the area of the triangle whose vertices are (6, 3), (−3, 5) and (4, −2) (ii) (at12, 2at1), (at22, 2at2) and (at32, 2at3) (iii) (a, c+a), (a, c) and (−a, c−a)
View SolutionFind the locus of the point (t2−t+1,t2+t+1),t∈R.
View SolutionFind the value of the products: (4a2+3b)(4a2+3b)at a=1, b=2.
View SolutionMatch te columns

(1) a-s, b-t, c-r, d-p
(2) a-t, b-q, c-r, d-p
(3) a-t, b-r, c-q, d-p
(4) a-t, b-r, c-p, d-q
View SolutionFigure given here shows the variation of velocity of a particle with time.
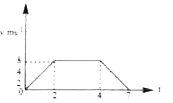
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
View SolutionLet S={a,b,c} and T={1,2,3}. Find F−1 of the following functions F from S to T, if it exists.(i) F={(a,3),(b,2),(c,1)}(ii) F={(a,2),(b,1),(c,1)}
View SolutionIf ∫10etdtt+1=a, then evaluate ∫bb−1etdtt−b−1
View Solution
